跳转至

机器学习在数据分析上的实际应用

约 1395 个字 1 张图片 预计阅读时间 5 分钟

Data Analysis

Data

  • data modalities: number, image, video, audio, text, graph, point cloud, etc.
  • data cleaning
  • data augmentation 增强

  • feature extraction/feature engineering

  • domain expertise

  • math tricks

    • kernel methods
    • principal component analysis
    • neural network
  • normalization/standardization
  • imbalanced data
  • data splitting

Attributes

Nomial

Ordinal序数

Interval

Ratio 比率

Algorithm / Model

discriminative vs. generative supervised vs. unsupervised classification vs. regression linear vs. nonlinear

Evaluation

Testing Metrics

  • accuracy, recall, precision, receiver, operator curve

  • Truth/Prediction True False
    True True Positive False Negative
    False False Negative True Negative
\[ accuracy=\frac{TP+TN}{TP+TN+FP+FN}, recall=\frac{TP}{TP+FN}, precision=\frac{TP}{TP+FP}, F_1=\frac{2*recall*precison}{recall+precision} \]
  • mean squared error

Training Metrics

  • mean squared error, cross entropy loss
  • mean squared error

Probability & Statistics

Pobability

Probability Statistics
Events Population
Trial Sample
Numerical characteristics of random variables Numerical characteristics
Asymptotic theory Statistical inference

Distributions

Bernoulli distribution 伯努利分布

  1. Binary Outcomes: It has only two possible outcomes. For example, flipping a coin results in either heads or tails.

  2. Parameters: The distribution is characterized by a single parameter p, which is the probability of success (where 0≤p≤1).

  3. Random Variable: A random variable X that follows a Bernoulli distribution takes the value 1 with probability p(success) and the value 0 with probability 1−p(failure).

  4. Mean and Variance:

  • Mean (Expected Value): E(X)=p
  • Variance: Var(X)=p(1−p)

  1. Usage: This distribution is used to model scenarios with two outcomes, such as pass/fail, yes/no, win/lose, etc. It's a fundamental building block for more complex distributions like the Binomial distribution, which models the number of successes in a fixed number of independent Bernoulli trials.

  2. Probability Mass Function (PMF): The PMF of a Bernoulli distributed random variable

\[ \begin{align*} P(X = k) = \begin{cases} p & \text{if } k = 1 \\ 1-p & \text{if } k = 0 \end{cases} \end{align*} \]

Binomial distribution 二项分布

  1. Trials: The distribution is defined by the number of trials, n, which is a fixed number.

  2. Success Probability: The probability of success on an individual trial, p.

  3. Random Variable: A random variable X following a Binomial distribution represents the number of successes in n trials.

  4. Mean and Variance: - Mean (Expected Value): E(X)=np* - Variance: Var(X)=np(1−p)

  5. Probability Mass Function (PMF): The probability of getting exactly k successes in n trials is given by:

\[ \begin{align*} P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} \end{align*} \]
  1. Usage: The Binomial distribution is used widely in statistics, particularly for modeling the number of successes in various scenarios such as flipping a coin, quality control processes, survey responses, and other fields where the outcomes are binary and trials are independent.

Normal distribution/Gaussian distribution 正态分布

Key Features

  1. Shape: The Normal distribution is bell-shaped and symmetric about its mean.

  2. Mean (μ): This is the central location of the distribution and is also the median and mode.

  3. Standard Deviation (σ): This measures the dispersion or variability around the mean; 68% of the data falls within one σ standard deviation of the mean, 95% within two σ, and 99.7% within three σ, a property known as the empirical rule or 68-95-99.7 rule.

  4. Formula: The probability density function (PDF) of the Normal distribution for a random variable X is given by:

\[ \begin{align*} f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \end{align*} \]
1
μ 是平均值，σ 是标准差standard deviation
  1. Applications: The Normal distribution is used for various applications including:
  • Statistical inference
  • Prediction intervals
  • Process control
  • Natural phenomena (e.g., measurement errors, heights of people)
  1. Central Limit Theorem: This fundamental theorem in statistics states that the sum (or average) of a large number of independent, identically distributed variables with finite means and variances will approximately follow a Normal distribution, regardless of the underlying distribution.

Properties

  • Skewness 偏度: The Normal distribution has a skewness of zero, indicating a perfectly symmetrical shape.
  • Kurtosis 峰度: It has a kurtosis of 3, which is the baseline for comparing the peakedness of other distributions (mesokurtic中峰度).

Uniform distribution 均匀分布

均匀分布是另一种简单但有用的概率分布。 它模拟了一个场景，其中所有结果在一定范围内发生的可能性相同。 该分布是在两个参数 a 和 b 之间定义的，它们分别是最小值和最大值。

  • Continuous: Unlike the Bernoulli or Binomial distributions, the Uniform distribution is continuous.

  • Range: The outcomes are uniformly distributed over the interval [a,b].

  • Probability Density Function (PDF): The PDF of the Uniform distribution is given by:

\[ \begin{align*} f(x) = \frac{1}{b-a} \quad \text{for} \quad x \in [a, b] \end{align*} \]

This indicates that every point in the interval [a,b] has the same probability density.

  • Mean and Variance:

  • Mean (Expected Value): \((a+b)/2\)

  • Variance: $$ \frac{(b-a)^2}{12} $$

Poisson distribution 泊松分布

泊松分布是一种概率分布，它对固定时间或空间间隔内发生的事件数量进行建模，前提是这些事件以已知的恒定平均速率发生，并且与自上次事件以来的时间无关。

  1. Parameter λ: The average number of events per interval, λ (lambda), is the rate at which events happen. It's the only parameter of this distribution.

  2. Discrete Distribution: The Poisson distribution is used for discrete events (e.g., counting the number of emails received in an hour).

  3. Probability Mass Function (PMF): The PMF of a Poisson distributed random variable X indicating the probability of observing exactly k events is given by:

\[ \begin{align*} P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \end{align*} \]

for k=0,1,2,…, where e is the base of the natural logarithm.

  1. Mean and Variance:
  • Mean: λ
  • Variance: λ
  1. Applications

The Poisson distribution is widely used in various fields such as:

  • Telecommunications (e.g., number of phone calls per minute)
  • Traffic engineering (e.g., cars passing a point)
  • Biology (e.g., mutations in a strand of DNA)
  • Queueing theory

Beta distribution

beta 分布是在区间 [0, 1] 上定义的一系列连续概率分布，由两个正形状参数（用 α 和 β 表示）进行参数化。 它在统计、贝叶斯分析和机器学习等领域特别有用。

1.Support: The distribution is defined for values on the interval [0, 1].

2.Shape Parameters: α and β control the shape of the distribution:

  • If α=β=1, the beta distribution is uniform.

  • If α>1 and β=1 (or vice versa), the distribution is skewed towards 1 (or 0).

  • If α=β>1, the distribution is symmetric and bell-shaped around 0.5.

  • If α<1 and β<1, the distribution is U-shaped.

3.Mean: The mean of the beta distribution is \(\frac{\alpha}{\alpha+\beta}\).

4.Variance: The variance is \(\frac{α+β}{(α+β)^2(α+β+1)}\)​.

5.Probability Density Function (PDF):

\[ f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \]

Where:

  • x is the variable over the interval [0, 1].
  • α and β are shape parameters.
  • B(α,β) is the beta function, serving as a normalization factor.
Example

​ In Bayesian data analysis, if the prior distribution for a parameter 0 is Beta(2, 2), and after observing data, the posterior distribution is Beta(5, 3), what is the maximum a posteriori (MAP) estimate for 0?

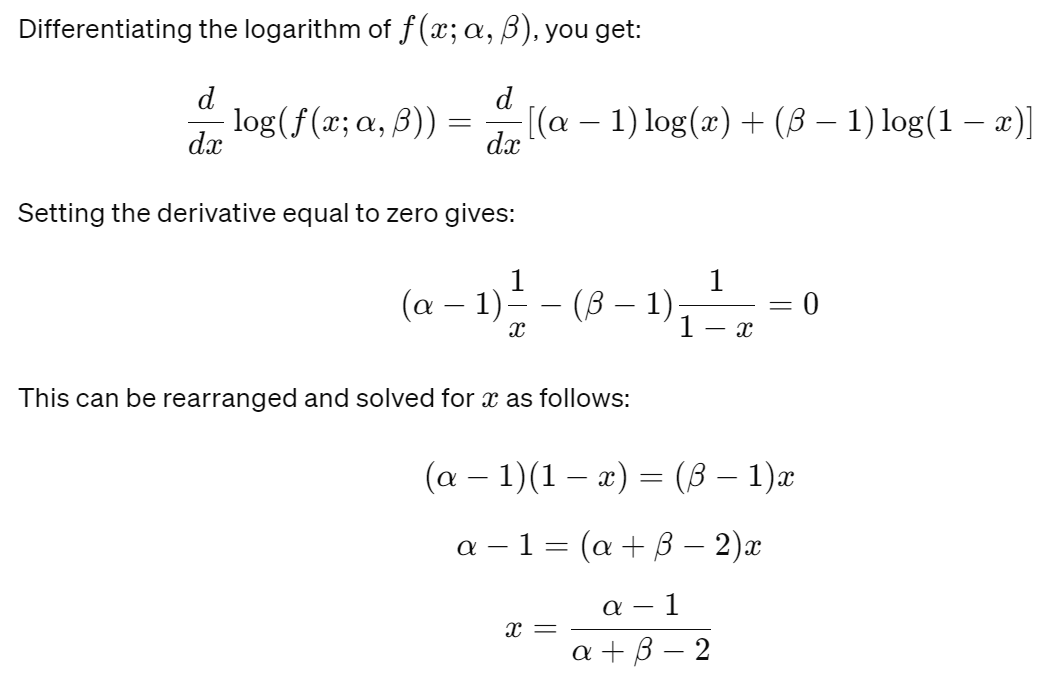
image-20240414172044383

​ Given a posterior distribution Beta(5, 3), let's plug in the values α=5 and β=3 into the formula to calculate the MAP estimate. The maximum a posteriori (MAP) estimate for the parameter x is approximately 0.67.

Statistics

  • The concept of population and sample

  • Statistics

  • sample mean
  • sample variance
  • Statistical inference
  • Frequentist view \(P(D;θ)\)​
  • Point estimation
    • Methods
    • maximum likelihood estimation(MLE)
    • method of moments
    • Evaluation of methods
    • consistency
    • unbiasedness
    • minimum-variance

Bayesian Theorem

Bayesian view \(P(D|θ)\)

  • realtions between events

  • subsetting(inclusion) and equality

  • mutuak exclusion and negation
    • Addition Law of Probability
    • Total Probability

  • operations on events

  • addition(union)

  • multiplication(intersection)
  • subtraction(difference)

  • Conditional probability

  • independence among events

    • Multiplication law of Probability

Bayesian equation $$ P(\theta|D)=\frac{P(D|\theta)P(\theta)}{P(D)}\ \ posterior=\frac{likelihood*prior}{evidence} $$

Bayesian inference

  • Maximum A Posterior(MAP)
\[ \theta^* = \mathop{argmax}_{\theta}\, P(\theta|D)=\mathop{argmax}_{\theta}\, P(D|\theta)P(\theta) \]
  • Minimum Mean Squared Error
\[ \theta^* = \mathop{argmin}_{\theta}\mathop{E}_{\hat{\theta}-posterior} {(\hat{\theta}-\theta)}^2=\mathop{E}_{\hat{\theta}-posterior}[\hat{\theta}] \]

https://chat.openai.com/share/80223f00-4ab2-41d5-8691-db83547f1ff9

Null hypothesis testing

假设检验

the null hypothesis is denoted by \(H_0\)​

Type 1 error, Type 2 error:

https://chat.openai.com/share/0cd19f6f-30c4-47c1-8506-70572dfead58

Unsupervised Learning

Clustering

K-means

anomly

symbols to meaning

SVD(single value decomposition)

PCA(Principal components analysis): use only the top k columns of U and V

latent semantic analysis

Supervised learning

Classification

https://chatgpt.com/share/1d5a433a-f924-4e02-b700-e9aaecb9cbdf

评论区~

有用的话请给我个赞和 star => GitHub stars