ECE498/598 Deep Generative Models¶
约 1166 个字 1 张图片 预计阅读时间 4 分钟
Overview¶
VAE(Variational Autoencoder)/Latent space models
- 智能的压缩与解压 (Encoding & Decoding) 变分自编码器
- All images have a latent set of rules \(z∈R^K\),\(k≤N\) from which they are generated.
- Learning the distribution of the rules \(q_{\alpha}(z)\) is all we need.
- z is the hidden rule 编码要有规律,尽可能地像一个标准的高斯分布,
- We can sample from that distribution \(q_{\alpha}(z)\) and generate images based on those sampled rules.
- Conditional distribution: \(q_{\alpha}(z=\text{rules}|x=\text{chess board images})\) decode rules into images
- Encoder: rule generator
GANs
- 博弈与对抗 (Adversarial Game)
- Learn transformation from white noise to real images. Instead, train model A to synthesize real-looking images
- Train model B to discriminate that model A is generating fake images. Train both models A and B jointly.
Diffusion
- 先污染,后治理 (Denoising Process)
- Let’s transform given data points progressively to Gaussian noise
- Then, learn how to remove the noise to get back to the data points. Once trained, this model will be able to transform samples from Gaussian to samples of data.
Flows
- 可逆的数学变换 (Invertible Transformation)
- No need to make noise and then denoise
- Think of the problem through the lens of ODE / SDE. We want to learn a vector field so that initial points (from a Gaussian) …will follow a trajectory and end up at points on the data distribution.
| 特征维度 | VAE (变分自编码器) | GANs (生成对抗网络) | Diffusion (扩散模型) | Flows (流模型) |
|---|---|---|---|---|
| 核心机制 | 编码-解码,学习潜在空间的概率分布 | 对抗博弈,生成器与判别器相互竞争 | 迭代去噪,从噪声中逐步恢复图像 | 可逆变换,学习简单与复杂分布间的精确映射 |
| 生成速度 | 快 (一次前向传播) | 快 (一次前向传播) | 非常慢 (需要成百上千次迭代) | 快 (一次前向传播) |
| 图像质量 | 一般,偏模糊 | 高,图像锐利 | 极高,当前最佳 | 中等,数学上优美但效果常有限制 |
| 训练稳定性 | 非常稳定 | 不稳定,需要小心调参 | 稳定 | 稳定 |
| 潜在空间 | 结构性好,平滑连续,适合插值和编辑 | 结构性不明确,需要额外技术 (如StyleGAN) | 潜在表示与噪声水平相关 | 结构性好,与简单分布一一对应 |
Probability Review¶
Fundemetal¶
Likelihood: you know this distribution, so easy to calculate
Posterior: the opposite is a known distribution, but this is a bit harder
| Likelihood | p(data | distribution parameters ) | Tractable, well defined |
| Posterior | p (distribution parameters | data ) | Typical goal, tricky, try Bayes |
| Prior | p( distribution parameters ) | Domain knowledge |
| Evidence | p(data) | Approximate with large data |
Maximum likelihood Estimation(MLE)¶
- Slide the bell curve towards the position that maximizes the probability of all data points.
- 为了求解 θargmaxL(θ), 我们需要解方程: δθδL(θ)=0
Expectation Maximization (EM)
Multivariate Gaussian Distribution 多元高斯分布¶
Multivariate Gaussian distribution/joint normal distribution $$ p(x)=\frac1{\sqrt(2π)^k∣Σ∣}exp(−\frac12(x−μ)⊤Σ^{−1}(x−μ)) $$ 这个公式是多元正态分布(也叫高斯分布)的概率密度函数 (Probability Density Function, PDF)
\(\mathbf {X} \ \sim \ {\mathcal {N}}_{k}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})\)
- \(p(x)\): represents the probability density of the occurrence of data point x 概率密度
- \(μ\): the mean vector of the distribution均值向量, representing the center of the distribution
- \(Σ\): the covariance matrix of the distribution 协方差矩阵, representing the degree of dispersion of the data and the correlation between different dimensions
- \(|Σ|\): the determinant of the covariance matrix 协方差矩阵的行列式
- \(Σ^{−1}\): the inverse of the covariance matrix 协方差矩阵的逆矩阵
- exp(⋅): the natural exponential function e(⋅) 自然指数函数
Normal distribution 正太分布¶
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is $$ f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$ - \(\text{Notation: }{\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}\\\) - \(f(x)=\text{probability density function}\\\) - \(\sigma =\text{standard deviation}\\\) - \(\mu =\text{mean}\)
Here’s a breakdown of each component of the notation:
-
x: This represents the random variable. It's a variable whose value is a numerical outcome of a random phenomenon, like the height of a randomly selected person or the result of a measurement.
-
~: This symbol is shorthand for "is distributed as" or "follows the distribution of." It connects the random variable to the specific probability distribution that describes its behavior.
-
N: This stands for the Normal distribution, also known as the Gaussian distribution. It's arguably the most important probability distribution in statistics. Its probability density function creates a perfectly symmetric, bell-shaped curve.
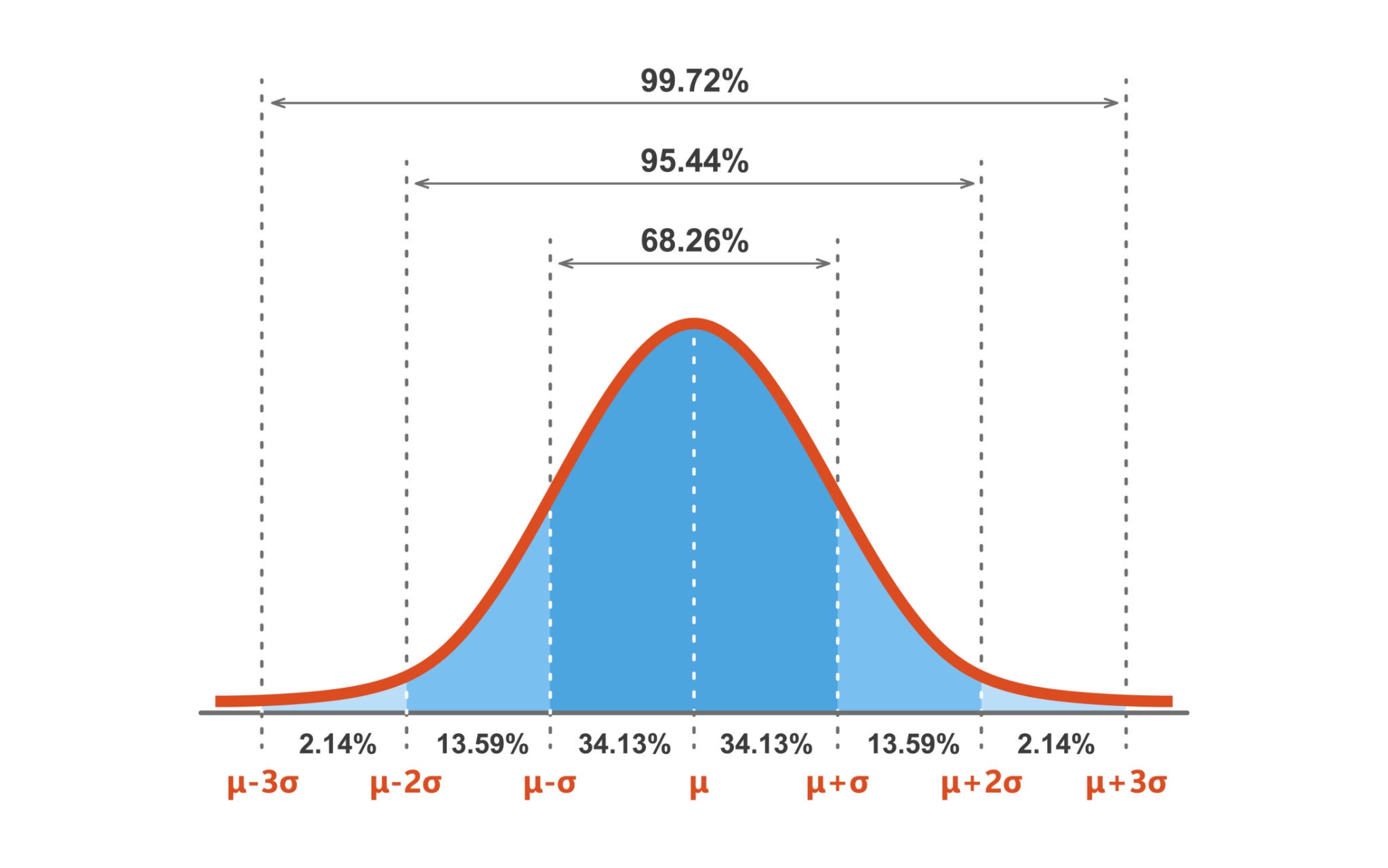
- μ (mu): This is the mean of the distribution. For a normal distribution, the mean represents:
- The center or central tendency of the data.
- The peak of the bell curve.
-
The expected value or average of the random variable x.
-
σ^2 (sigma-squared): This is the variance of the distribution. The variance measures the spread or dispersion of the data around the mean μ.
-
A small variance means the data points are tightly clustered around the mean, resulting in a tall and narrow bell curve.
- A large variance means the data points are spread out, resulting in a short and wide bell curve.
- The square root of the variance, σ, is called the standard deviation. It's often easier to interpret because it's in the same units as the mean.
Uniform probability distribution¶
\(U(0,θ)\) means that a random variable can take on any value between 0 and θ with equal probability. For any value outside of this range, the probability is zero. Unlike a Normal distribution's bell curve, the graph of a Uniform distribution's probability is a simple rectangle.
- U: Stands for Uniform.
- 0: The minimum possible value the variable can take.
- θ: The maximum possible value the variable can take.
- Probability function: $$ L(θ∣x)=\begin{cases} \left( \frac{1}{\theta} \right)^n, & \text{if } \theta \geq \max(x_i) \ 0, & \text{otherwise} \end{cases}$$
