数据结构基础 Fudemental Data Structure

约 5459 个字 1018 行代码 4 张图片 预计阅读时间 31 分钟

引论

ADT abstract data type 抽象数据类型
\(O(N)≤\)
\(Ω(N)≥\)
\(Θ(N)=\)
\(o(N)＜\)

排序 sort

stable 稳定: A sorting algorithm is said to be stable if two items with equal keys _in the same order _in the sorted output as they appear in the input array. That is, the order of elements with identical keys is preserved.

Quick Sort 快速排序

Quick Sort is a sorting algorithm that works using the divide-and-conquer approach. It chooses a pivot places it in its correct position in the sorted array and partitions the smaller elements to its left and the greater ones to its right. This process is continued for the left and right parts and the array is sorted.
两边分组排序
时间复杂度：\(O(N logN)\)平均
每一轮排序 run 都有一个数 pivot 被放到最终正确的位置上
The position of the pivot element is finalized after each partitioning.

Heap Sort 堆排序

Heap Sort - Data Structures and Algorithms Tutorials - GeeksforGeeks
Heap sort is a comparison-based sorting technique based on Binary Heap data structure. It is similar to the selection sort where we first find the minimum element and place the minimum element at the beginning. Repeat the same process for the remaining elements.
首先使用 heapify (percolate down) 将数组转换为堆数据结构，然后逐个删除 Max-heap 的根节点，将其替换为堆中的最后一个节点，然后堆化堆的根。重复此过程，直到堆的大小大于 1。

• 从给定的输入数组构建堆。
• 重复以下步骤，直到堆只包含一个元素：
• 将堆的根元素（即最大的元素）与堆的最后一个元素交换。
• 删除堆的最后一个元素（现在位于正确位置）。
• 堆砌堆的其余元素。
• 排序后的数组是通过反转输入数组中元素的顺序来获得的。

性质：unstable
时间复杂度：\(O(N)\)??

code

#include <stdio.h>

// Function to swap the position of two elements
void swap(int* a, int* b)
{

    int temp = *a;
    *a = *b;
    *b = temp;
}

// To heapify a subtree rooted with node i
// which is an index in arr[].
// n is size of heap
void heapify(int arr[], int N, int i)
{
    // Find largest among root,
    // left child and right child

    // Initialize largest as root
    int largest = i;

    // left = 2*i + 1
    int left = 2 * i + 1;

    // right = 2*i + 2
    int right = 2 * i + 2;

    // If left child is larger than root
    if (left < N && arr[left] > arr[largest])

        largest = left;

    // If right child is larger than largest
    // so far
    if (right < N && arr[right] > arr[largest])

        largest = right;

    // Swap and continue heapifying
    // if root is not largest
    // If largest is not root
    if (largest != i) {

        swap(&arr[i], &arr[largest]);

        // Recursively heapify the affected
        // sub-tree
        heapify(arr, N, largest);
    }
}

// Main function to do heap sort
void heapSort(int arr[], int N)
{

    // Build max heap
    for (int i = N / 2 - 1; i >= 0; i--)

        heapify(arr, N, i);

    // Heap sort
    for (int i = N - 1; i >= 0; i--) {

        swap(&arr[0], &arr[i]);

        // Heapify root element
        // to get highest element at
        // root again
        heapify(arr, i, 0);
    }
}

// A utility function to print array of size n
void printArray(int arr[], int N)
{
    for (int i = 0; i < N; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// Driver's code
int main()
{
    int arr[] = { 12, 11, 13, 5, 6, 7 };
    int N = sizeof(arr) / sizeof(arr[0]);

    // Function call
    heapSort(arr, N);
    printf("Sorted array is\n");
    printArray(arr, N);
}

Insertion Sort 插入排序

Insertion Sort - Data Structure and Algorithm Tutorials - GeeksforGeeks
Insertion sort is a simple sorting algorithm that works similarly to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
若要按升序对大小为 N 的数组进行排序，请遍历该数组并将当前元素（键）与其前一个元素进行比较，如果关键元素小于其前一个元素，请将其与之前的元素进行比较。将较大的元素向上移动一个位置，以便为交换的元素腾出空间。
时间复杂度：

// C++ program for insertion sort
#include <bits/stdc++.h>
using namespace std;
// Function to sort an array using insertion sort
void insertionSort(int arr[], int n)
{
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];

        // Move elements of arr[0..i-1],
        // that are greater than key, 
        // to one position ahead of their
        // current position
        for ( j=i; j>0 && arr[j-1] > key; j--){
            arr[j] = arr[j-1];
        }
        arr[j] = key;
    }
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
    int i;
    for (i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << endl;
}

// Driver code
int main()
{
    int arr[] = { 12, 11, 13, 5, 6 };
    int N = sizeof(arr) / sizeof(arr[0]);

    insertionSort(arr, N);
    printArray(arr, N);

    return 0;
}
// This is code is contributed by rathbhupendra

Shell Sort 希尔排序

Shell sort is mainly a variation of Insertion Sort. In insertion sort, we move elements only one position ahead. When an element has to be moved far ahead, many movements are involved. The idea of ShellSort is to allow the exchange of far items. In Shell sort, we make the array h-sorted for a large value of h. We keep reducing the value of h until it becomes 1. An array is said to be h-sorted if all sublists of every h’th element are sorted.
分组 h-插入排序
性质： unstable
时间复杂度：
Algorithm:
Step 1 − Start
Step 2 − Initialize the value of gap size. Example: h.
Step 3 − Divide the list into smaller sub-part. Each must have equal intervals to h.
Step 4 − Sort these sub-lists using insertion sort.
Step 5 – Repeat this step 2 until the list is sorted.
Step 6 – Print a sorted list.
Step 7 – Stop.

void Shellsort( ElementType A[ ], int N ) 
{ 
      int  i, j, Increment; 
      ElementType  Tmp; 
      for ( Increment = N / 2; Increment > 0; Increment /= 2 )  
    /*h sequence */
    for ( i = Increment; i < N; i++ ) { /* insertion sort */
          Tmp = A[ i ]; 
          for ( j = i; j >= Increment; j - = Increment ) 
        if( Tmp < A[ j - Increment ] ) 
              A[ j ] = A[ j - Increment ]; 
        else 
              break; 
        A[ j ] = Tmp; 
    } /* end for-I and for-Increment loops */
}

Hibbard 增量序列
\(H_k=2^k-1\), 且其最坏情形下运行时间为 \(O(N^{3/2})\)

Selection Sort 选择排序

Merge Sort 归并排序

性质： stable
时间复杂度：\(O(N logN)\)

// C program for Merge Sort
#include <stdio.h>
#include <stdlib.h>
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    // Create temp arrays
    int L[n1], R[n2];

    // Copy data to temp arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // Merge the temp arrays back into arr[l..r
    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of L[],
    // if there are any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy the remaining elements of R[],
    // if there are any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// l is for left index and r is right index of the
// sub-array of arr to be sorted
void mergeSort(int arr[], int l, int r)
{
    if (l < r) {
        int m = l + (r - l) / 2;

        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        merge(arr, l, m, r);
    }
}

// Function to print an array
void printArray(int A[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}

// Driver code
int main()
{
    int arr[] = { 12, 11, 13, 5, 6, 7 };
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr, arr_size);

    mergeSort(arr, 0, arr_size - 1);

    printf("\nSorted array is \n");
    printArray(arr, arr_size);
    return 0;
}

Bucket Sort 桶排序

间接/表排序

排序的元素是结构大，移动指针数组进行排序
N 个数字的排列一定是由若干个独立的环组成的

• 每访问一个环，当table[i]==i时环结束

时间复杂度：（最坏）向下取整 N/2 个环，每个环包括两个元素； 总\(O(M*n)\)，M 是每个元素 A 复制的时间

Q

1. If there are less than 20 inversions in an integer array, then Insertion Sort will be the best method among Quick Sort, Heap Sort and Insertion Sort. T
2. For the quicksort implementation with the left pointer stops at an element with the same key as the pivot during the partitioning, but the right pointer does not stop in a similar case, what is the running time when all keys are equal?
3. \(O(logN)\)
4. \(O(N)\)
5. \(O(NlogN)\)
6. \(O(N^2)\)

The running time is \(O(n^2)\) in the worst case [6]. This is because in such a situation, the partitioning doesn't effectively divide the array into smaller subproblems, leading to a degenerate case where the algorithm essentially performs a linear scan. Quicksort's typical efficiency relies on dividing the problem into subproblems, and when this doesn't occur due to equal keys, the algorithm's performance degrades.（answer from AI）

3. To sort { 49, 38, 65, 97, 76, 13, 27, 50 } in increasing order, which of the following is the result after the 1^st run of Shell sort with the initial increment 4?
4. 13,27,38,49,50,65,76,97
5. 49,13,27,50,76,38,65,97
6. 49,76,65,13,27,50,97,38
7. 97,76,65,50,49,38,27,13

First Pass (Increment 4):

• Compare elements at positions 1 and 5 (49 and 76), no swap needed.
• Compare elements at positions 2 and 6 (38 and 13), swap.
• Compare elements at positions 3 and 7 (65 and 27), swap.
• Compare elements at positions 4 and 8 (97 and 50), swap.
• if not present due to length, no swap needed. 4. Among the following sorting methods, which ones will be slowed down if we store the elements in a linked structure instead of a sequential structure?

1. Insertion sort; 2. Select ion Sort; 3. Bubble sort; 4. Shell sort; 5. Heap sort

2. 1 and 2 only

3. 2 and 3 only
4. 3 and 4 only
5. 4 and 5 only

Heap sort是在数组中, heap本身在数组中, shell sort也是在数组中， 链表查询较慢

5. To sort N elements by heap sort, the extra space complexity is: \(O(1)\)
6. During the sorting, processing every element which is not yet at its final position is called a "run". To sort a list of integers using quick sort, it may reduce the total number of recursions by processing the small partion first in each run. **F **

希望平均分，处理两个都一样的

7. 
   

散列 hashing

冲突 collision：Two elements with different keys share the same hash value
装填因子 load factor: \(λ=n/tablesize\)
散列平均查找期望是\(O(1)\)，几乎与关键字空间 n 无关

• 以较小的装填因子为前提，以空间换时间
• 不便于顺序查找关键字、范围查找、最大最小值查找等

分离链接法

把所有有冲突的 key 用链表串联在一起
装填因子可能超过 1，成功查找期望略大于不成功
链表储存效率和查找效率比较低
关键字删除不需要“懒惰删除”法
太小的装填因子可能浪费空间，太大将付出时间代价

开放定址法

如果发生第 i 次冲突，探测的下一个地址+di
装填因子越大，（不）成功查找期望次数越大（指数级增长，不成功>成功）；装填因子较小时，各种期望探测次数都不大且比较接近。
散列表是个数组，储存效率高，随机查找，有聚集现象

线性探测法 Linear probing

\(di=i\)
平均查找长度（次数）一般失败>成功
成功查找长度 ASLs：散列中每个元素要找 xi 次（xi=冲突次数+1），相加取平均（➗实际哈希表元素个数）
失败查找长度 ASLu：找不在散列中的元素，对于每个哈希值 h(x)， 照样 mod + 后移找，若是遇到空格则证明不在散列中，此时的查找次数 xi 相加取平均

平方探测法 Quadratic probing

增量序列：1，-1，\(2^2\)，\(-2^2\)，\(3^2\)，\(-3^2\), …… ,\(q^2\),\(-q^2\)且 \(q≤⌊tablesize/2⌋\)
可能出现表有位置但找不到的情况（\(i^2\)也一样 )
使用平方探测法：
当表的大小是素数且表有一半是空的的时候，总能插入一个新的元素
如果表的大小是形如 4k+3 的素数，使用 \(F(i)=+-i^2\)，那么整个表都能被探测到

Q

1. Which of the following statements about HASH is true?
2. the expected number of probes for insertions is greater than that for successful searches in linear probing method
3. insertions are generally quicker than deletions in separate chaining method
4. if the table size is prime and the table is at least half empty, a new element can always be inserted with quadratic probing
5. all of the above
6. The average search time of searching a hash table with N elements is:
7. \(O(1)\)
8. \(O(logN)\)
9. \(O(N)\)
10. cannot be determined

表 List

Q

For a sequentially stored linear list of length N, the time complexities for query and insertion are O(1) and O(N), respectively. T

栈 stack

栈（Stack）：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。
Last-in-First-out

void Push(Elementstype X, Stack S){
    PtrtoNode Tmp;
    //略去判断是不是NULL
    Tmp->Element=X;
    Tmp->Next=S->Next;//换表头
    S->Next=Tmp;
}
void Pop(Stack S){
    PtrtoNode first;
    //略去判断是不是空
    first=S->Next;
    S->Next=S->Next->Next;//换表头
    free(first);
}

void Push(Stack S){
    //略去判断是不是满了
    S->Array[++S->TopOfStack]=X;
}
void Pop(Stack S){
    //略去判断是不是空
    S->TopOfStack--;
}

Q

• Stacks and queues are lists with insertion/deletion constraints.

队列 queue

First-in-first-out
circular array
检测队列是不是空是很重要的

Q

Suppose that an array of size m is used to store a circular queue. If the front position is front and the current size is size, then the rear element must be at (front+size-1)%m.

树 Tree

深度 根 到 节点 ni （根的深度为 0，树的深度是它最深树叶的深度）
高度 节点 ni 到叶子 （树的高度是根的高度）
路径 节点的一个顺序，一棵树中从根到每个节点恰好存在一条路径

Binary Tree

度数为 0 的节点 = 度数为 2 的节点+1

完全二叉树 complete binary tree

The parent of a node at index _i _ is located at index \(⌊i/2⌋\)

insert 插入

如果队列里没有 X，Insert(Elemnettype X, SearchTree T)将 X 插入到遍历路径的最后一点上

二叉查找树 Binary Search Tree（BST）

左边都比根小，右边都比根大
树的平均深度 \(O(Nlog N)\)

Delete

左子树最大或者右子树最小的数来代替被删掉的节点（不是叶子

ternary tree 三叉树

The number of leaf nodes in a ternary tree (三叉树) is only related to the number of degree 2 nodes and that of degree 3 nodes, namely, it has nothing to do with the number of degree 1 nodes.

Perfect binary tree 理想二叉树

满二叉树，是一种特殊类型的二叉树。在理想二叉树中，除了叶子节点之外，每个节点都有两个子节点，且所有叶子节点都位于同一层次上。这使得理想二叉树具有良好的平衡性。

Q

1. In a complete binary tree with 1102 nodes, there must be __ leaf nodes.
2. 79
3. 551
4. 1063
5. cannot be determined - n 为偶数，leaf nodes 的数量=\(n/2\); n 为奇数，leaf nodes 的数量=\((n+1)/2\)
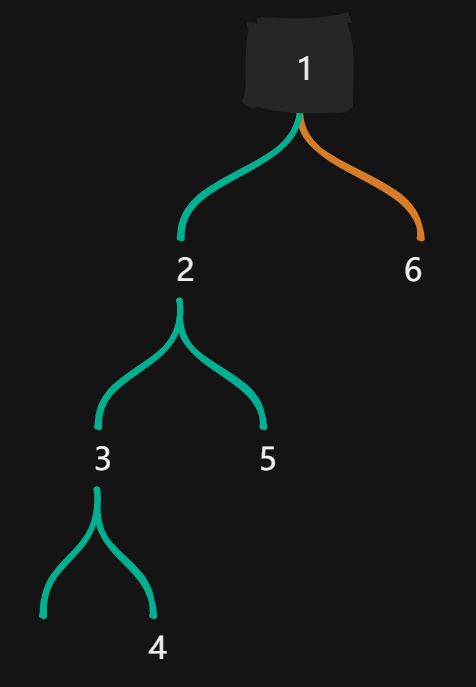
6. In-order traversal of a binary tree can be done iteratively. Given the stack operation sequence as the following:push(1), push(2), push(3), pop(), push(4), pop(), pop(), push(5), pop(), pop(), push(6), pop()

Which one of the following statements is TRUE?

1. 6 is the root
2. 2 is the parent of 4
3. 2 and 6 are siblings
4. None of the above - 入栈顺序即为先序遍历的顺序，出栈顺序即为中序遍历的顺序 - 入栈 123456 出栈 342516

re

Tree BuildTree( int in[], int pre[], int N )
{ //in[] stores the inorder traversal sequence
//and pre[] stores the preorder traversal sequence
//N is the number of nodes in the tree
    Tree T;
    int i;
    if (!N) {
    return NULL;
    }
    T = (Tree)malloc(sizeof(struct Node));
    T->Data = pre[0];
    for (i=0; i<N; i++)
        if (in[i]==T->Data) break;
    T->Left = BuildTree( in, pre+1, i);
    T->Right = BuildTree( in+i+1, pre+i+1, N-i-1);
    return T;
}

Tree BuildTree( int in[], int post[], int N )
{ 
    Tree T;
    int i;
    if (!N) {
    return NULL;
    }
    T = (Tree)malloc(sizeof(struct Node));
    T->Data = post[N-1];
    for (i=0; i<N; i++)
        if (in[i]==T->Data) break;
    T->Left = BuildTree( in, post, i);
    T->Right = BuildTree( in+i+1, post+i+1, N-i);
    return T;
}

堆 Heap 优先队列

堆序性 heap order

• the nodes along the path from the root to any node are in sorted order

二叉堆 binary heap 是完全填满的二叉树 complete binary tree
节点数 \(2^h\)~\(2^h-1\)
高度 h \(⌊logN⌋\)
父亲在\(⌊i/2⌋\)位置上

Insert

上滤 percolate up

在下一个空的位置建一个空穴，向根的方向上走，直到能放入 X

假设 heap的高度为h, binary tree最多有2^(h+1) - 1 个 nodes. 因此新插入一个node最多需要log(n+1) -1 次比较. big O is \(O(logN)\)​

DeleteMin

下滤 percolate down

将删除元素中儿子的较小值放入空穴，空穴下移一层，重复操作，直到最后一个元素放到正确的位置上（要满足完全二叉树）

Build

用 Insert， O(N)，最优方法采用的是递归，自下而上的build

IncreaseKey

void IncreaseKey( int P, int D, PriorityQueue H )
{
   int i, key;
   key = H->Elements[P] + D;
   for ( i = P; H->Elements[i/2] < key; i/=2 )     
        H->element[i]=H->Element[i/2];
   H->Elements[i] = key;
}

DecreaseKey

void DecreaseKey( int P, int D, PriorityQueue H )
{
    int i, key;
    key = H->Elements[P] - D;
    for ( i = P; H->Elements[i/2] > key; i/=2 )
        H->Elements[i] = H->Elements[i/2];
    H->Elements[i] = key;
}

关系 Relation

等价关系 equivalence relation

• 自反性 reflexive
• 对称性 symmetric
• 传递性 transitive

eg. 相似、模运算、图像连通性

等价类 equivalence class

对于 集合 S 有 n 个元素，等价类 equivalence class 数量 x， 有 1≤x≤n 个
等价类形成对 S 的一个划分：S 的每个成员恰好出现在一个等价类中

不相交 disjoint

Union/Find 算法（并查算法）

array[] 中每个元素存的是它的根节点的值
Introduction to Disjoint Set (Union-Find Algorithm) - GeeksforGeeks

Find

Find(i) O(X)与 X 节点的深度成正比 返回等价类名字（当且仅当两个元素属于相同集合时，Find 返回相同名字

// Finds the representative of the set
// that i is an element of
#include<bits/stdc++.h>
using namespace std;

int find(int i)
{
    // If i is the parent of itself
    if (parent[i] == i) {
        // Then i is the representative of
        // this set
        return i;
    }
    else {
        // Else if i is not the parent of
        // itself, then i is not the
        // representative of his set. So we
        // recursively call Find on its parent
        return find(parent[i]);
    }
}
// The code is contributed by Nidhi goel

Find ( ElementType X, DisjSet S )
{   
    ElementType root, trail, lead;

    for ( root = X; S[root] > 0; root=S[root]) ;  
    for ( trail = X; trail != root; trail = lead ) {
        lead = S[trail] ;   
        S[trail]=root;   
    } 
    return root;
}

Union

Union(a,b) Θ(N) 将 a 和 b 两个等价类合并成一个新的等价类
Union(a,b)后新的根是 a

// Unites the set that includes i
// and the set that includes j

#include <bits/stdc++.h>
using namespace std;

void union(int i, int j) {
    // Find the representatives
    // (or the root nodes) for the set
    // that includes i
    int irep = this.Find(i),
    // And do the same for the set
    // that includes j
    int jrep = this.Find(j);
    // Make the parent of i’s representative
    // be j’s representative effectively
    // moving all of i’s set into j’s set)
    this.Parent[irep] = jrep;
}

union-by-size 按大小求并

小的并到大的上
任何节点的深度 depth 不会超过\(log(N)\)
\(height(T)≤⌊log_2 N⌋ +1\)

union-by-height 按高度求并

任何节点的深度 depth ≤ 不会超过\(log(N)\)

路径压缩 path compression

在 Find 操作中执行， 从 X 到根的路径上的每一个节点都使它的父节点变成根，即 使 S[X] 的值等于 Find 返回的值
路径压缩与按大小求并完全兼容

SetType Find ( ElementType X, DisjSet S )
{   
   ElementType root, trail, lead;

   for ( root = X; S[root] > 0; root=S[root]) ;  
   for ( trail = X; trail != root; trail = lead ) {
      lead = S[trail] ;   
      S[trail]=root;   
   } 
   return root;
}

//The function BuildMinHeap(H, K) is to arrange elements H[1] ... H[K] into a min-heap. 
//Please complete the following program.

ElementType FindKthLargest ( int A[], int N, int K )
{   /* it is assumed that K<=N */
    ElementType *H;
    int i, next, child;

    H = (ElementType *)malloc((K+1)*sizeof(ElementType));
    for ( i=1; i<=K; i++ ) H[i] = A[i-1];
    BuildMinHeap(H, K);

    for ( next=K; next<N; next++ ) {
        H[0] = A[next];
        if ( H[0] > H[1] ) {
            for ( i=1; i*2<=K; i=child ) {
                child = i*2;
                if ( child!=K && H[child+1]<H[child] ) child++;
                if ( H[0] > H[child] )
                    H[i] = H[child];
                else break;
            }
            H[i] = H[0];
        }
    }
    return H[1];
}

Q

1. The array representation of a disjoint set is given by { 4, 6, 5, 2, -3, -4, 3 }. If the elements are numbered from 1 to 7, the resulting array after invoking Union(Find(7),Find(1)) with union-by-size and path-compression is:
2. { 4, 6, 5, 2, 6, -7, 3 }
3. { 4, 6, 5, 2, -7, 5, 3 }
4. { 6, 6, 5, 6, -7, 5, 5 }
5. { 6, 6, 5, 6, 6, -7, 5 } #####

图 Graph

introduction

In a directed graph, the sum of the in-degrees and out-degrees of all the vertices is twice the total number of edges.
求和 degree=2E
有最多的边的数量有向图是 n(n-1) ,无向图是 n(n-1) /2*

connected

There are n vertices.
The minimum number of edges in a connected graph is (n-1). The maximum for this question is (n-1) (n-2)/2 + 1. This is because (n-1) edges can be connected by maximum (n-1) (n-2)/2 edges, and 1 edge to connect to the lonely vertex.

割点 articulation point/cut vertex

A vertex v is an articulation point (also called cut vertex) if removing v increases the number of connected components.

拓扑排序 topological

对有向无圈图的顶点的一种排序

Dijkstra algorithm

找到从一个给定点到所有点之间的最短路径
时间复杂度：\(O(|E|+|V|^2)\)

Maximum Network Flow 最大网络流

给定一个表示流网络的图，其中每条边都有容量。还给定图中的两个顶点源“s”和汇“t”，在以下约束下找到从 s 到 t 的最大可能流量：

1. 边缘上的流量不会超过边缘的给定容量。
2. 对于除 s 和 t 之外的每个顶点，传入流等于传出流。

Dinic

Dinic’s algorithm for Maximum Flow - GeeksforGeeks
Dinic 的算法使用以下概念：

1. 将残差图 G 初始化为给定图。
2. 对 G 进行 BFS 来构造一个级别图（或将级别分配给顶点），并检查是否可以有更多流。
3. 如果无法获得更多流量，则返回
4. 使用级别图在 G 中发送多个流，直到达到 阻塞流。_这里使用级别图意味着，在每个流中，从 s 到 t，路径节点的级别应该是 0、1、2…（按顺序）。

时间复杂度 \(O(EV^2)\)

// C++ implementation of Dinic's Algorithm
#include <bits/stdc++.h>
using namespace std;

// A structure to represent a edge between
// two vertex
struct Edge {
    int v; // Vertex v (or "to" vertex)
        // of a directed edge u-v. "From"
        // vertex u can be obtained using
        // index in adjacent array.

    int flow; // flow of data in edge

    int C; // capacity

    int rev; // To store index of reverse
            // edge in adjacency list so that
            // we can quickly find it.
};

// Residual Graph
class Graph {
    int V; // number of vertex
    int* level; // stores level of a node
    vector<Edge>* adj;

public:
    Graph(int V)
    {
        adj = new vector<Edge>[V];
        this->V = V;
        level = new int[V];
    }

    // add edge to the graph
    void addEdge(int u, int v, int C)
    {
        // Forward edge : 0 flow and C capacity
        Edge a{ v, 0, C, (int)adj[v].size() };

        // Back edge : 0 flow and 0 capacity
        Edge b{ u, 0, 0, (int)adj[u].size() };

        adj[u].push_back(a);
        adj[v].push_back(b); // reverse edge
    }

    bool BFS(int s, int t);
    int sendFlow(int s, int flow, int t, int ptr[]);
    int DinicMaxflow(int s, int t);
};

// Finds if more flow can be sent from s to t.
// Also assigns levels to nodes.
bool Graph::BFS(int s, int t)
{
    for (int i = 0; i < V; i++)
        level[i] = -1;

    level[s] = 0; // Level of source vertex

    // Create a queue, enqueue source vertex
    // and mark source vertex as visited here
    // level[] array works as visited array also.
    list<int> q;
    q.push_back(s);

    vector<Edge>::iterator i;
    while (!q.empty()) {
        int u = q.front();
        q.pop_front();
        for (i = adj[u].begin(); i != adj[u].end(); i++) {
            Edge& e = *i;
            if (level[e.v] < 0 && e.flow < e.C) {
                // Level of current vertex is,
                // level of parent + 1
                level[e.v] = level[u] + 1;

                q.push_back(e.v);
            }
        }
    }

    // IF we can not reach to the sink we
    // return false else true
    return level[t] < 0 ? false : true;
}

// A DFS based function to send flow after BFS has
// figured out that there is a possible flow and
// constructed levels. This function called multiple
// times for a single call of BFS.
// flow : Current flow send by parent function call
// start[] : To keep track of next edge to be explored.
//       start[i] stores count of edges explored
//       from i.
// u : Current vertex
// t : Sink
int Graph::sendFlow(int u, int flow, int t, int start[])
{
    // Sink reached
    if (u == t)
        return flow;

    // Traverse all adjacent edges one -by - one.
    for (; start[u] < adj[u].size(); start[u]++) {
        // Pick next edge from adjacency list of u
        Edge& e = adj[u][start[u]];

        if (level[e.v] == level[u] + 1 && e.flow < e.C) {
            // find minimum flow from u to t
            int curr_flow = min(flow, e.C - e.flow);

            int temp_flow
                = sendFlow(e.v, curr_flow, t, start);

            // flow is greater than zero
            if (temp_flow > 0) {
                // add flow to current edge
                e.flow += temp_flow;

                // subtract flow from reverse edge
                // of current edge
                adj[e.v][e.rev].flow -= temp_flow;
                return temp_flow;
            }
        }
    }

    return 0;
}

// Returns maximum flow in graph
int Graph::DinicMaxflow(int s, int t)
{
    // Corner case
    if (s == t)
        return -1;

    int total = 0; // Initialize result

    // Augment the flow while there is path
    // from source to sink
    while (BFS(s, t) == true) {
        // store how many edges are visited
        // from V { 0 to V }
        int* start = new int[V + 1]{ 0 };

        // while flow is not zero in graph from S to D
        while (int flow = sendFlow(s, INT_MAX, t, start)) {

            // Add path flow to overall flow
            total += flow;
        }

        // Remove allocated array
        delete[] start;
    }

    // return maximum flow
    return total;
}

// Driver Code
int main()
{
    Graph g(6);
    g.addEdge(0, 1, 16);
    g.addEdge(0, 2, 13);
    g.addEdge(1, 2, 10);
    g.addEdge(1, 3, 12);
    g.addEdge(2, 1, 4);
    g.addEdge(2, 4, 14);
    g.addEdge(3, 2, 9);
    g.addEdge(3, 5, 20);
    g.addEdge(4, 3, 7);
    g.addEdge(4, 5, 4);

    // next exmp
    /*g.addEdge(0, 1, 3 );
    g.addEdge(0, 2, 7 ) ;
    g.addEdge(1, 3, 9);
    g.addEdge(1, 4, 9 );
    g.addEdge(2, 1, 9 );
    g.addEdge(2, 4, 9);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 5, 3);
    g.addEdge(4, 5, 7 );
    g.addEdge(0, 4, 10);

    // next exp
    g.addEdge(0, 1, 10);
    g.addEdge(0, 2, 10);
    g.addEdge(1, 3, 4 );
    g.addEdge(1, 4, 8 );
    g.addEdge(1, 2, 2 );
    g.addEdge(2, 4, 9 );
    g.addEdge(3, 5, 10 );
    g.addEdge(4, 3, 6 );
    g.addEdge(4, 5, 10 ); */

    cout << "Maximum flow " << g.DinicMaxflow(0, 5);
    return 0;
}

Ford-

MST 最小生成树

最小生成树(MST) 或带权连通无向图的最小权重生成树是权重小于或等于所有其他生成树权重的生成树。

Necessary-And-Sufficient-Condition-for-Unique-MST

Necessary-And-Sufficient-Condition-for-Unique-MST
Let 𝐺 _be a connecte d weighted graph and _𝑇 a minimum spanning tree of 𝐺. Show that 𝑇 is a unique minimum spanning tree if and only if the weight of each edge 𝑒 _of _𝐺 that is not in 𝑇 exceeds the weight of every other edge on the cycle in 𝑇+𝑒 .

1. Existence of Minimum Spanning Tree (MST): - If the graph is connected, a minimum spanning tree always exists. - For an undirected connected graph, the minimum spanning tree is a subset of edges that forms a tree connecting all vertices with the minimum possible total edge weight.
2. Conditions for Existence: - In a connected graph, a minimum spanning tree is guaranteed. - If the graph is not connected, there won't be a minimum spanning tree [4].
3. Algorithms: - Kruskal's and Prim's algorithms are commonly used to find the minimum spanning tree of a connected graph.

Prim 算法

从已经在 MST 里面的顶点中，连接未在 MST 中的顶点，使其边权最小
Step 1: Determine an arbitrary vertex as the starting vertex of the MST.
Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST (known as fringe vertex).
Step 3: Find edges connecting any tree vertex with the fringe vertices.
Step 4: Find the minimum among these edges.
Step 5: Add the chosen edge to the MST if it does not form any cycle.
Step 6: Return the MST and exit

// A C program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph

#include <limits.h>
#include <stdbool.h>
#include <stdio.h>

// Number of vertices in the graph
#define V 5

// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(int key[], bool mstSet[])
{
    // Initialize min value
    int min = INT_MAX, min_index;

    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
            min = key[v], min_index = v;

    return min_index;
}

// A utility function to print the
// constructed MST stored in parent[]
int printMST(int parent[], int graph[V][V])
{
    printf("Edge \tWeight\n");
    for (int i = 1; i < V; i++)
        printf("%d - %d \t%d \n", parent[i], i,
            graph[i][parent[i]]);
}

// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
    // Array to store constructed MST
    int parent[V];
    // Key values used to pick minimum weight edge in cut
    int key[V];
    // To represent set of vertices included in MST
    bool mstSet[V];

    // Initialize all keys as INFINITE
    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;

    // Always include first 1st vertex in MST.
    // Make key 0 so that this vertex is picked as first
    // vertex.
    key[0] = 0;

    // First node is always root of MST
    parent[0] = -1;

    // The MST will have V vertices
    for (int count = 0; count < V - 1; count++) {

        // Pick the minimum key vertex from the
        // set of vertices not yet included in MST
        int u = minKey(key, mstSet);

        // Add the picked vertex to the MST Set
        mstSet[u] = true;

        // Update key value and parent index of
        // the adjacent vertices of the picked vertex.
        // Consider only those vertices which are not
        // yet included in MST
        for (int v = 0; v < V; v++)

            // graph[u][v] is non zero only for adjacent
            // vertices of m mstSet[v] is false for vertices
            // not yet included in MST Update the key only
            // if graph[u][v] is smaller than key[v]
            if (graph[u][v] && mstSet[v] == false
                && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }

    // print the constructed MST
    printMST(parent, graph);
}

// Driver's code
int main()
{
    int graph[V][V] = { { 0, 2, 0, 6, 0 },
                        { 2, 0, 3, 8, 5 },
                        { 0, 3, 0, 0, 7 },
                        { 6, 8, 0, 0, 9 },
                        { 0, 5, 7, 9, 0 } };

    // Print the solution
    primMST(graph);

    return 0;
}

时间复杂度：\(O(V^2)\)，如果输入图使用邻接表来表示，那么借助二叉堆，Prim算法的时间复杂度可以降低到\(O(E * logV)\)。在这个实现中，我们总是考虑生成树从图的根开始
空间：\(O(V)\)

Kruskal 算法

Kruskal’s Minimum Spanning Tree (MST) Algorithm - GeeksforGeeks
在克鲁斯卡尔算法中，按升序对给定图的所有边进行排序。如果新添加的边不形成环，则继续在MST中添加新的边和节点。它首先选择最小加权边，最后选择最大加权边。因此我们可以说它在每一步中都做出局部最优选择以找到最优解。因此这是一个贪婪算法。

1. 按权重非降序对所有边进行排序。
2. 选择最小的边。检查是否与目前形成的生成树形成环。如果未形成循环，则包括该边。否则，丢弃它。
3. 重复步骤2，直到生成树中有 (V-1) 条边。

   // C++ program for the above approach 
   
   #include <bits/stdc++.h> 
   using namespace std; 
   
   // DSU data structure 
   // path compression + rank by union 
   class DSU { 
       int* parent; 
       int* rank; 
   
   public: 
       DSU(int n) 
       { 
           parent = new int[n]; 
           rank = new int[n]; 
   
           for (int i = 0; i < n; i++) { 
               parent[i] = -1; 
               rank[i] = 1; 
           } 
       } 
   
       // Find function 
       int find(int i) 
       { 
           if (parent[i] == -1) 
               return i; 
   
           return parent[i] = find(parent[i]); 
       } 
   
       // Union function 
       void unite(int x, int y) 
       { 
           int s1 = find(x); 
           int s2 = find(y); 
   
           if (s1 != s2) { 
               if (rank[s1] < rank[s2]) { 
                   parent[s1] = s2; 
               } 
               else if (rank[s1] > rank[s2]) { 
                   parent[s2] = s1; 
               } 
               else { 
                   parent[s2] = s1; 
                   rank[s1] += 1; 
               } 
           } 
       } 
   }; 
   
   class Graph { 
       vector<vector<int> > edgelist; 
       int V; 
   
   public: 
       Graph(int V) { this->V = V; } 
   
       // Function to add edge in a graph 
       void addEdge(int x, int y, int w) 
       { 
           edgelist.push_back({ w, x, y }); 
       } 
   
       void kruskals_mst() 
       { 
           // Sort all edges 
           sort(edgelist.begin(), edgelist.end()); //边排序
   
           // Initialize the DSU 
           DSU s(V); 
           int ans = 0; 
           cout << "Following are the edges in the "
                   "constructed MST"
               << endl; 
           for (auto edge : edgelist) { 
               int w = edge[0]; 
               int x = edge[1]; 
               int y = edge[2]; 
   
               // Take this edge in MST if it does 
               // not forms a cycle 
               if (s.find(x) != s.find(y)) { 
                   s.unite(x, y); 
                   ans += w; 
                   cout << x << " -- " << y << " == " << w 
                       << endl; 
               } 
           } 
           cout << "Minimum Cost Spanning Tree: " << ans; 
       } 
   }; 
   
   // Driver code 
   int main() 
   { 
       Graph g(4); 
       g.addEdge(0, 1, 10); 
       g.addEdge(1, 3, 15); 
       g.addEdge(2, 3, 4); 
       g.addEdge(2, 0, 6); 
       g.addEdge(0, 3, 5); 
   
       // Function call 
       g.kruskals_mst(); 
   
       return 0; 
   }
   

   时间复杂度：\(O(E * logE)\) 或 \(O(E * logV)\)

• 边排序需要 \(O(E * logE)\) 时间。
• 排序后，我们迭代所有边并应用查找并集算法。查找和并集操作最多需要 \(O(logV)\) 时间。
• 所以总体复杂度是 \(O(E * logE + E * logV)\) 时间。
• E的值最多可以是O(V 2 )，因此O(logV)和O(logE)是相同的。因此，总体时间复杂度为 \(O(E * logE)\)或 \(O(E*logV)\)

DFS 深度优先搜索

1. 最初堆栈和访问数组都是空的。
2. 访问某一节点，将其未访问过的相邻节点放入栈中。
3. 访问栈顶并将其从栈中弹出，并将其所有未访问的相邻节点放入栈中。
4. 重复步骤 3 直到栈变空，DFS 结束

Find articulation point 找割点

Strongly Connected Components 强连通组件

Tarjan 算法 找割点？还是强连通组件

DFS+栈实现
哔哩哔哩视频参考

#include<malloc.h>
typedef struct VNode *PtrToVNode;
struct VNode {
    Vertex Vert;
    PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
    int NumOfVertices;
    int NumOfEdges;
    PtrToVNode *Array;
};

int count=0;
#define min(a,b) (((a)<(b))?(a):(b))
void find(Graph G, Vertex v, int num[],int low[], PtrToVNode stack, int visited[]);
void push(int x, PtrToVNode s);
int top(PtrToVNode s);
void pop(PtrToVNode s);
void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) ){
    int low[MaxVertices]={0};
    int visited[MaxVertices]={0};
    int num[MaxVertices]={0};
    PtrToVNode stack;
    stack=malloc(sizeof(struct VNode));
    for (int i = 0; i < G->NumOfVertices; i++) {
        if (num[i] == 0) {
            find(G, i,num,low,stack,visited);
        }
    }
}
void find(Graph G, Vertex v, int num[],int low[], PtrToVNode stack, int visited[]){
    visited[v]=1;
    num[v] = low[v] = count++;
    push(v,stack);
    PtrToVNode w;
    for(w=G->Array[v];w!=NULL;w=w->Next){
        if(!num[w->Vert]){
            find(G,w->Vert,num,low,stack,visited);

            low[v]=min(low[v],low[w->Vert]);
        }
        else if(visited[w->Vert]){
                low[v]=min(low[v],num[w->Vert]);
            }

    }
    if(num[v]==low[v] ){
        int t;
        while(1){
            if(t!=v ){
                t=top(stack);
                pop(stack);
                visited[t]=0;
                printf("%d ",t);
            }else {
                printf("\n");
                break;
            }
        }

    }
}
void push(int x, PtrToVNode s){
    PtrToVNode tmp;
    tmp=malloc(sizeof(struct VNode));
    if(tmp!=NULL){
        tmp->Vert=x;
        tmp->Next=s->Next;
        s->Next=tmp;
    }
}
int top(PtrToVNode s){
    if(s->Next!=NULL){
        return s->Next->Vert;
    }
    return 0;
}
void pop(PtrToVNode s){
    PtrToVNode a;
    a=malloc(sizeof(struct VNode));
    if(s->Next!=NULL){
        a=s->Next;
        s->Next=s->Next->Next;
        free(a);
    }
}

时间复杂度：\(O(E+V)\)邻接表；\(O(V^2)\)邻接矩阵

Q

1. If an undirected graph G = (V, E) contains 10 vertices. Then to guarantee that G is connected in any cases, there has to be at least __ edges. ？
2. 45
3. 37
4. 36
5. 9
6. Which of the following statements is TRUE about topological sorting?
7. If a graph has a topological sequence, then its adjacency matrix must be triangular.
8. If the adjacency matrix is triangular, then the corresponding directed graph must have a unique topological sequence.
9. In a DAG, if for any pair of distinct vertices Vi and Vj, there is a path either from Vi to Vj or from Vj to Vi, then the DAG must have a unique topological sequence.
10. If Vi precedes Vj in a topological sequence, then there must be a path from Vi to V
11. Let P be the shortest path from S to T. If the weight of every edge in the graph is incremented by 2, P will still be the shortest path from S to T. F

4. The minimum spanning tree of any connected weighted graph: 任意连通加权图的最小生成树
   C.may not be unique
5. Apply DFS to a directed acyclic graph（有向无圈图）, and output the vertex before the end of each recursion. The output sequence will be:

C.reversely topologically sorted

6. Graph G is an undirected completed graph of 20 nodes. Is there an Euler circuit in G? If not, in order to have an Euler circuit, what is the minimum number of edges which should be removed from G?

Each Node has exactly 19 degrees

• Euler Circuit (Strong Form) requires every node to be even degrees
• Euler Tour (Weak Form) requires 0 or 2 odd degrees

Remove 1 edge, every 2 nodes will lose 1 degrees, so we lose 10 edges

Questions

homework

1. For a sequentially stored linear list of length N, the time complexities for deleting the first element and inserting the last element are O(1) and O(N), respectively. F O(N) and O(1) - 顺序存储的线性表支持随机存取，所以查询的时间是常数时间，但插入需要把后面每一个元素的位置都进行调整，所以是线性时间。 插入最后一个时间为O(1).
2. 循环队列满时rear == front -1. enqueue时 rear 增加, dequeue front 增加.
3. To insert s after p in a doubly linked circular list, we must do:
   • A. p->next=s; s->prior=p; p->next->prior=s ;
   • B. p->next->prior=s; p->next=s; s->prior=p; s->next=p->next;
   • C. s->prior=p; s->next=p->next; p->next=s; p->next->prior=s;
   • D. s->prior=p; s->next=p->next; p->next->prior=s; p->next=s;
4. It is always possible to represent a tree by a one-dimensional integer array. T - It is always possible to represent a tree by a one-dimensional integer array using various techniques such as breadth-first or depth-first traversal.

5. If a general tree T is converted into a binary tree BT, then which of the following BT traversals gives the same sequence as that of the post-order traversal of T?

   • A. Pre-order traversal
   • B. In-order traversal
   • C. Post-order traversal
   • D. Level-order traversal
     T的preorder = BT的preorder
     T的postorder = BT的inorder

6. Among the following threaded binary trees (the threads are represented by dotted curves), which one is the postorder threaded tree?

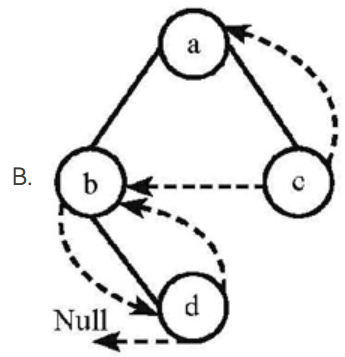
线索二叉树中，左线索为上一个结点，右线索为下一个结点

后序：左右根
中序：左根右
前序：根左右

1. Suppose that an array of size 6 is used to store a circular queue, and the values of front and rear are 0 and 4, respectively. Now after 2 dequeues and 2 enqueues, what will the values of front and rear be?
2. 2 and 0
3. 2 and 2
4. 2 and 4
5. 2 and 6 - 头是 0 而不是 6
6. Suppose that an array of size m is used to store a circular queue. If the head pointer front and the current size variable size are used to represent the range of the queue instead of front and rear, then the maximum capacity of this queue can be: (5分)
7. m-1
8. m
9. m+1
10. cannot be determined - 就是数组的大小

Midterm

1. The time comlexity of Selection Sort will be the same no matter we store the elements in an array or a linked list. T
2. If N numbers are stored in a singly linked list in increasing order, then the average time complexity for binary search is O(logN). F 链表是不能使用折半查找的
3. The time complexity of Selection Sort will be the same no matter we store the elements in an array or a linked list. T
4. If a stack is used to convert the infix expression a+bc+(de+f)*g into a postfix expression, what will be in the stack (listing from the bottom up) when f is read?
5. +(+
6. +(*+
7. abcde
8. ++(+

中缀表达式转化为后缀表达式，转化的算法如下：

• 初始化一个栈
• 逐个读取元素（数字或者操作符）
• 如果遇到数字，直接输出
• 如果遇到操作符（不考虑括号），如果其优先级大于栈顶元素，就将栈顶弹出，并重复此步骤，否则将该操作符压入栈中（栈为空的时候也直接压栈即可）
• 如果遇到左括号"("，直接将其压入栈中，如果遇到右括号")"，循环弹出顶栈元素，直到左括号为止（左括号也需要弹出，右括号不需要压栈），并且输出所有被弹栈顶元素（左括号除外） 5. Suppose that a polynomial（多项式） is represented by a linked list storing its non-zero terms. Given two polynimials with N1 and N2 non-zero terms, and the highest exponents being M1 and M2, respectively. Then the time complexity for adding them up is: 1. O(N1×N2) 2. O(N1+N2) 3. O(M1×M2) 4. O(M1+M2) 6.
  

Pta code

True or Flase

算法竞赛基础训练题_判断题_it is always possible to represent a tree by a one_白术_竹苓的博客-CSDN博客

function

List Reverse( List L ){
    List head,node,temp;
    node=L->Next;
    while(node){
        temp=node->Next;
        node->Next=head;
        head=node;
        node=temp;
    }
    L->Next=head;
    return L;
}


typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
struct Node {
    ElementType Element;
    Position Next;
};

The function Reverse is supposed to return the reverse linked list of L, with a dummy header.

Polynomial Add( Polynomial a, Polynomial b ){
    Polynomial head,temp,node;
    if(a==NULL) return b;
    if(b==NULL) return a;
    node=(Polynomial)malloc(sizeof(Polynomial));
    head=node;
    a=a->Next;
    b=b->Next;
    while(b && a){
        temp=(Polynomial)malloc(sizeof(Polynomial));

        if(b->Exponent > a->Exponent){
            temp->Coefficient=b->Coefficient;
            temp->Exponent=b->Exponent;
            b=b->Next;
        }else if(b->Exponent < a->Exponent){
            temp->Coefficient=a->Coefficient;
            temp->Exponent=a->Exponent;
            a=a->Next;
        }else{
            temp->Coefficient=a->Coefficient + b->Coefficient;
            temp->Exponent=a->Exponent;
            a=a->Next;
            b=b->Next;
            if(temp->Coefficient==0) continue;
        }
        temp->Next=NULL;
        node->Next=temp;
        node=temp;
    }
    if(a) node->Next=a;
    if(b) node->Next=b;
    return head;
}

typedef struct Node *PtrToNode;
struct Node {
    int Coefficient;
    int Exponent;
    PtrToNode Next;
};
typedef PtrToNode Polynomial;
/* Nodes are sorted in decreasing order of exponents.*/  

void Print_NLT( Tree T,  int X ){
    if(T == NULL)return;//如果树为空，返回null

    //直接进行树的遍历，因为是从大到小输出不小于X的数
    //所以先遍历右子树，大于X的直接输出，再遍历左子树.
    Print_NLT(T->Right,X);
    if(T->Element>=X){
        printf("%d ",T->Element);
    }
    Print_NLT(T->Left,X);

}

int Isomorphic( Tree T1, Tree T2 ){
    if(T1==NULL && T2==NULL)return 1;
    if((T1==NULL&&T2!=NULL)||(T1!=NULL&&T2==NULL))return 0;
    else if(T1->Element != T2->Element)return 0;
    return (Isomorphic(T1->Left,T2->Left)&&Isomorphic(T1->Right,T2->Right)) || (Isomorphic(T1->Right,T2->Left)&&Isomorphic(T1->Left,T2->Right));
}

void PercolateUp( int p, PriorityQueue H )
{
    while (H->Elements[p] < H->Elements[p/2] && p>1)
    {
        int temp;
        temp=H->Elements[p];
        H->Elements[p]=H->Elements[p/2];
        H->Elements[p/2]=temp;
        p /=2;
    } 
}

void PercolateDown( int p, PriorityQueue H )
{
    while (H->Elements[p] > H->Elements[p*2] && 2*p <= H->Size )
    {
        int temp;
        temp=H->Elements[p];
        H->Elements[p]=H->Elements[p*2];
        H->Elements[p*2]=temp;
        p *=2;
    } 
}

数据结构与算法（周测1-算法分析） - nonlinearthink - 博客园

评论区~

有用的话请给我个赞和 star =>