ECE408/CS483 Applied Parallel Programming

约 1325 个字 154 行代码 18 张图片 预计阅读时间 6 分钟

https://canvas.illinois.edu/courses/60979/assignments/syllabus

https://uiuc.chat/ECE408FA25/chat

Introduction

CPU(central processing unit)

GPU(graphical processing unit)

Post-Dennard technology pivot – parallelism and heterogeneity

The Moore’s Law (Imperative) drove feature sizes down, doubling the number of transistors/unit area every 18-24 months

• Exponential increase in clock speed

Dennard Scaling (based on physics) drove clock speeds up

• ended around 2005-2006

multicore: execution speed of sequential programs

many-thread: execution throughput of parallel applications

CPU vs GPU

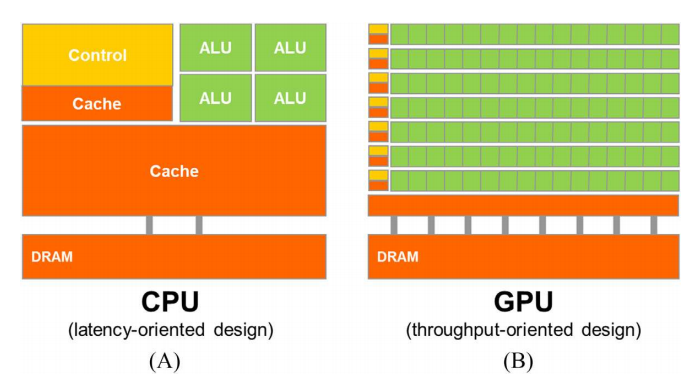
CPU	GPU
A few powerful ALUs(Arithmetic Logic Unit)	Many small ALUs
Reduced operation latency	Long latency, high throughput
Large caches	Heavily pipelined for further throughput
Convert long latency memory accesses to short latency cache accesses	Small caches
Sophisticated control	More area dedicated to computation
Branch prediction to reduce control hazards	Simple control
Data forwarding to reduce data hazards	More area dedicated to computation
Modest multithreading to hide short latency	A massive number of threads to hide the very high latency!
High clock frequency	Moderate clock frequency

CPUs for sequential parts where latency hurts

• CPUs can be 10+X faster than GPUs for sequential code

GPUs for parallel parts where throughput wins

• GPUs can be 10+X faster than CPUs for parallel code

Parallel Programming Frameworks

[!NOTE]

Why GPUs?

Why repurpose a graphics processing architecture instead of designing a throughput-oriented architecture from scratch?

• Chips are expensive to build and require a large volume of sales to amortize the cost
• This makes the chip market very difficult to penetrate
• When parallel computing became mainstream, GPUs already had (and still have) a large installed base from the gaming sector

Parallel Computing Challenges

Massive Parallelism demands Regularity -> Load Balance

Global Memory Bandwidth -> Ideal vs. Reality

Conflicting Data Accesses Cause Serialization and Delays

• Massively parallel execution cannot afford serialization
• Contentions in accessing critical data causes serialization

Parallel Computing Pitfall（陷阱）

Consider an application where:

1. The sequential execution time is 100s
2. The fraction of execution that is parallelizable is 90%
3. The speedup achieved on the parallelizable part is 1000×

What is the overall speedup of the application? $$ t_{parallel}=(1-0.9)\times 100s +\frac{0.9 \times 100s}{1000}=10.09s\ speedup=\frac{t_{sequential}}{t_{parallel}}=\frac{100s}{10.09s}=9.91\times \text{（9.91为倍数）} $$

Amdahl's Law

阿姆达尔定律：处理器并行运算之后效率提升的能力

The maximum speedup of a parallel program is limited by the fraction of execution that is parallelizable, namely, \(speedup<\frac{1}{1-p}\)

Introduction to CUDA C and Data Parallel Programming

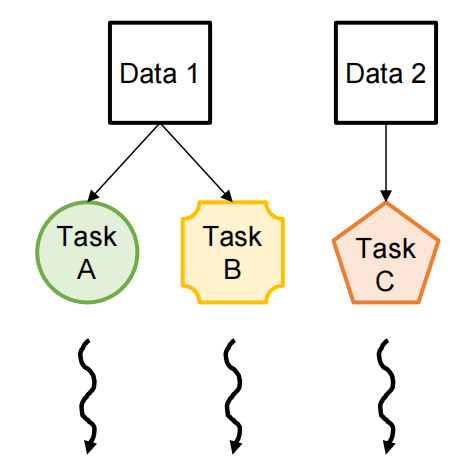
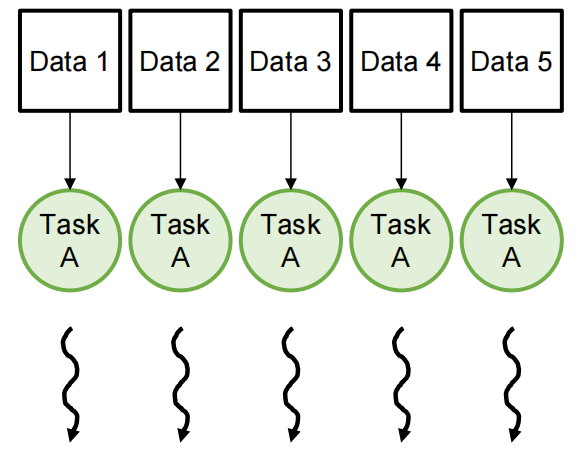
Types of Parallelism

Task Parallelism	Data Parallelism
Different operations performed on same or different data	Same operations performed on different data
Usually, a modest number of tasks unleashing a modest amount of parallelism	Potentially massive amounts of data unleashing massive amounts of parallelism(Most suitable for GPUs)

CUDA/OpenCL Execution Mode

Integrated Host +Device Application(C Program)

1. The execution starts with host code (CPU serial code).
2. When a kernel function is called, a large number of threads are launched on a device to execute the kernel. All the threads that are launched by a kernel call are collectively called a grid.
3. These threads are the primary vehicle of parallel execution in a CUDA platform
4. When all threads of a grid have completed their execution, the grid terminates, and the execution continues on the host until another grid is launched

• Host Code (C):Handles serial or modestly parallel tasks
• Device Kernel (C,SPMD Model):Executes highly parallel sections of the program

Threads

A CUDA kernel is executed as a grid(array) of threads

• All threads in the same grid run the same kernel
• Single Program Multiple Data (SPMD model)
• Each thread has a unique index that it uses to compute memory addresses and make control decisions

Thread as a basic unit of computing

• Threads within a block cooperate via shared memory, atomic operations and barrier synchronization. 块内的线程通过共享内存、原子操作和屏障同步进行协作。
• Threads in different blocks cooperate less.

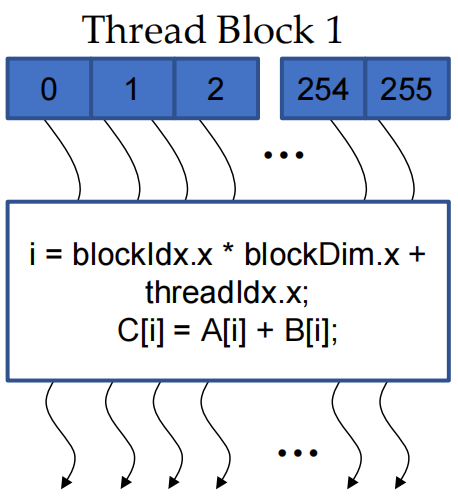
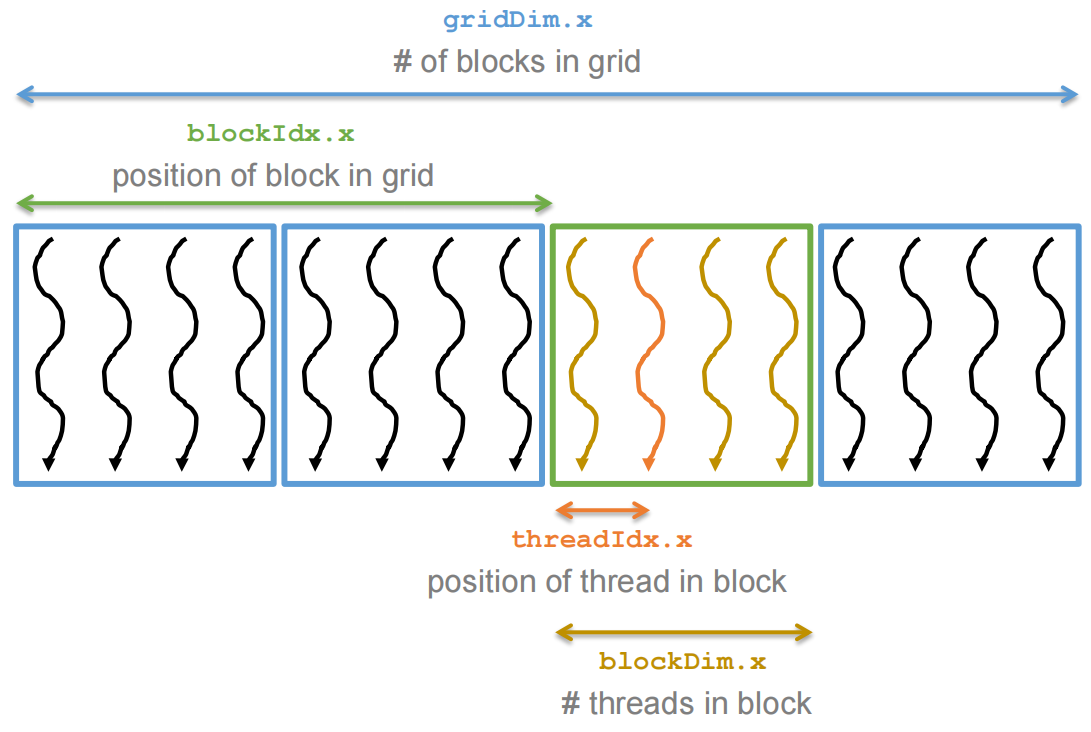
• Thread block and thread organization simplify memory addressing when processing multidimensional data

Vector Addition

We use vector addition to demonstrate the CUDA C program structure.

A simple traditional vector addition C code example.

// Compute vector sum C = A+B
void vecAdd(float* A, float* B, float* C, int n) {
    for (i = 0, i < n, i++) {
        C[i] = A[i] + B[i];
    }
}
int main() {
    // Memory allocation for A_h, B_h, and C_h
    // I/O to read A_h and B_h, N elements...
    vecAdd(A_h, B_h, C_h, N);
}

主机的变量名称后缀为_h，使用设备的变量名称后缀为_d

System Organization

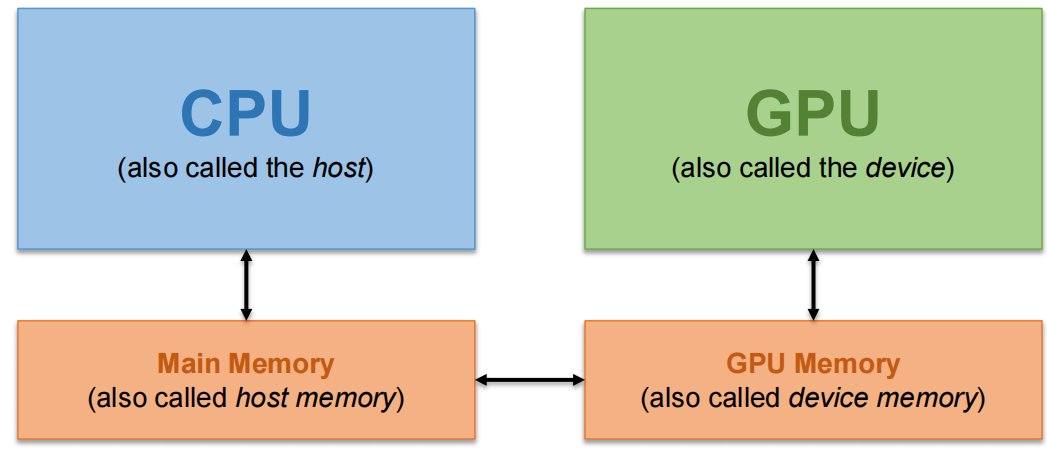
The CPU and GPU have separate memories and cannot access each others' memories

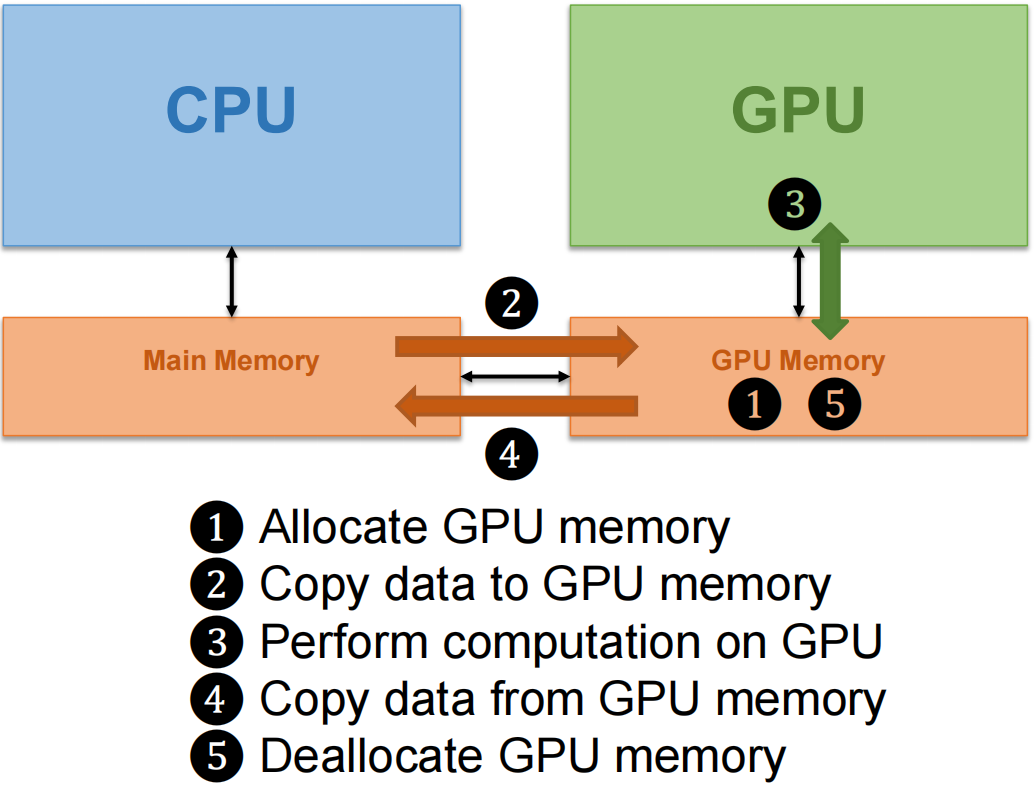
• Need to transfer data between them（下图五步操作）

A vector addition kernel

Outline of a revised vecAdd function that moves the work to a device.

#include <cuda.h>
void vecAdd(float* A, float* B, float* C, int n) {
int size = n* sizeof(float); 
float *A_d, *B_d, *C_d;
…
1. // Allocate device memory for A, B, and C
// copy A and B to device memory 
2. // Kernel launch code – to have the device
// to perform the actual vector addition
3. // copy C from the device memory
// Free device vectors

vector A + B = vector C

Device code can:

• R/W per-thread registers
• R/W per-grid global memory

Host code can transfer data to/from per grid global memory

CUDA Device Memory Management API

API for managing device global memory

Allocating memory

/*Allocating memory*/
cudaError_t cudaMalloc(void **devPtr, size_t size)
//devPtr: Pointer to pointer to allocated device memory
//size: Requested allocation size in byte

/*VecAdd Host Code*/
//详见下面

Deallocating memory

cudaError_t cudaFree(void *devPtr)
//devPtr: Pointer to device memory to free

• 指向设备全局内存中对象的指针变量后缀为_d
• A_d, B_d 和 C_d 中的地址指向设备全局内存 device global memory 中的位置。这些地址不应在主机代码中间接引用。它们应该在调用 API 函数和内核函数时使用。

Copying memory

cudaError_t cudaMemcpy(void *dst, const void *src, size_t count, enum cudaMemcpyKind kind)

//Example
cudaMemcpy(A_d, A_h, size, cudaMemcpyHostToDevice);
cudaMemcpy(B_d, B_h, size, cudaMemcpyHostToDevice);
. . . 
cudaMemcpy(C_h, C_d, size, cudaMemcpyDeviceToHost);

• dst: Destination memory address
• src: Source memory address
• count: Size in bytes to copy
• kind: Type of transfer
  • cudaMemcpyHostToHost
  • cudaMemcpyHostToDevice
  • cudaMemcpyDeviceToHost
  • cudaMemcpyDeviceToDevice

Return type: cudaError_t

• Helps with error checking (discussed later)

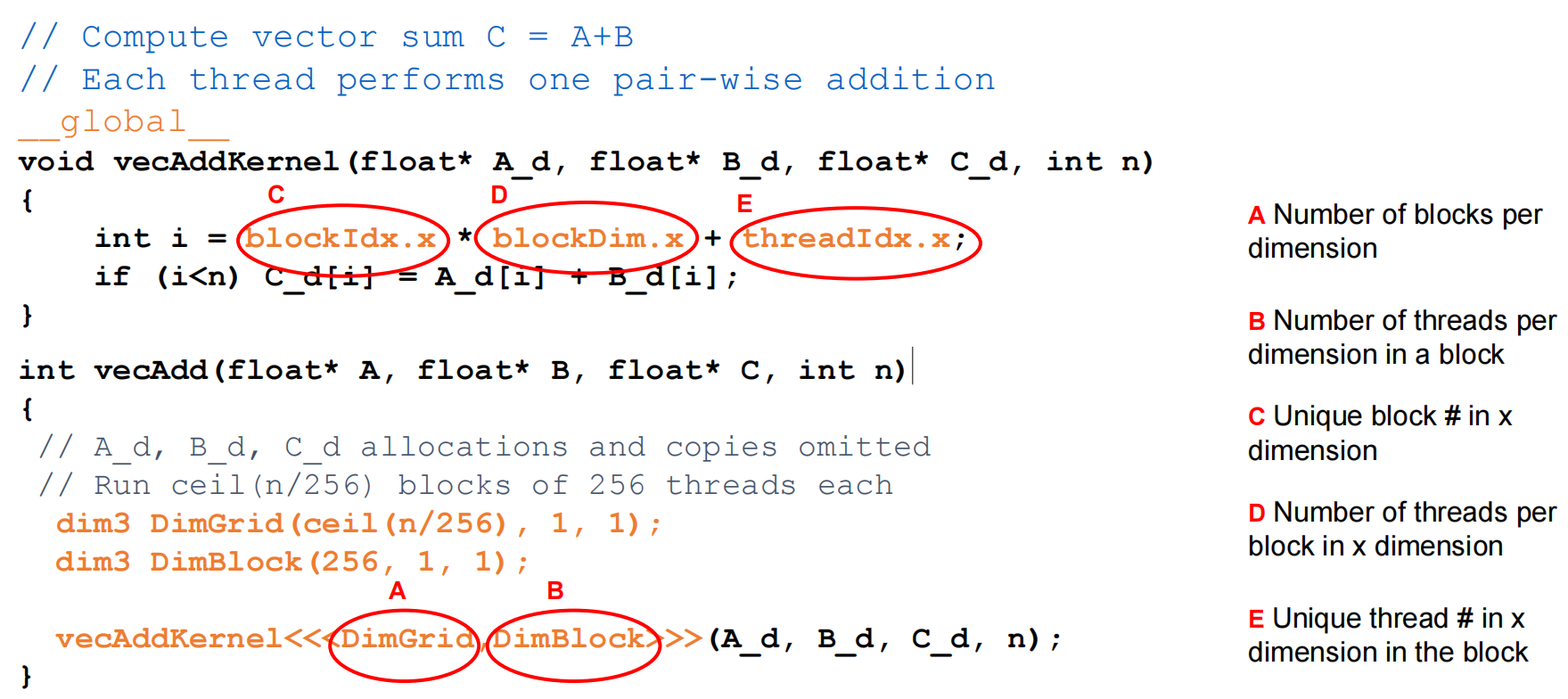
vecAdd Host Code

完整版本

void vecAdd(float* A, float* B, float* C, int n) {
    int size = n * sizeof(float); 
    float *A_d, *B_d, *C_d;
    // Transfer A and B to device memory (error-checking omitted)
    cudaMalloc((void **) &A_d, size);
    cudaMemcpy(A_d, A, size, cudaMemcpyHostToDevice);
    cudaMalloc((void **) &B_d, size);
    cudaMemcpy(B_d, B, size, cudaMemcpyHostToDevice);
    // Allocate device memory for
    cudaMalloc((void **) &C_d, size);
    // Kernel invocation code – to be shown later
        …

    // Transfer C from device to host
    cudaMemcpy(C, C_d, size, cudaMemcpyDeviceToHost);
    // Free device memory for A, B, C
    cudaFree(A_d); 
        cudaFree(B_d); 
    cudaFree(C_d);
}

Simple strategy of Parallel Vector Addition: assign one GPU thread per vector element

Launching a Grid

Threads in the same grid execute the same function known as a kernel

A grid can be launched by calling a kernel and configuring it with appropriate grid and block sizes:

const unsigned int numThreadsPerBlock = 512;
const unsigned int numBlocks = n/numThreadsPerBlock;
vecAddKernel <<< numBlocks, numThreadsPerBlock >>> (A_d, B_d, C_d, n);

If n is not a multiple of numThreadsPerBlock, fewer threads will be launched than desired

• Solution: use the ceiling to launch extra threads then omit the threads after the boundary:

vecAddKernel <<< ceil(n/256.0), 256 >>> (A_d, B_d, C_d, n);

More Ways to Compute Grid Dimensions

// Example #1
dim3 DimGrid(n/numThreadsPerBlock, 1, 1);
if (0 != (n % numThreadsPerBlock)) { DimGrid.x++; }
dim3 DimBlock(numThreadsPerBlock, 1, 1);
vecAddKernel<<<DimGrid, DimBlock>>>(A_d, B_d, C_d, n);
// Example #2
const unsigned int numBlocks;
numBlocks = (n + numThreadsPerBlock – 1)/numThreadsPerBlock;

vecAddKernel<<<numBlocks, numThreadsPerBlock>>>(A_d, B_d, C_d, n);

Vector Addition Kernel

// Compute vector sum C = A+B
// Each thread performs one pair-wise addition
__global__
    void vecAddKernel(float* A_d, float* B_d, float* C_d, int n)
{
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if (i<n) C_d[i] = A_d[i] + B_d[i];
}
int vecAdd(float* A, float* B, float* C, int n)
{
    // A_d, B_d, C_d allocations and copies omitted 
    // Run ceil(n/256) blocks of 256 threads each
    dim3 DimGrid(ceil(n/256), 1, 1);
    dim3 DimBlock(256, 1, 1);
    vecAddKernel<<<DimGrid,DimBlock>>>(A_d, B_d, C_d, n);
}

Compiling A CUDA Program

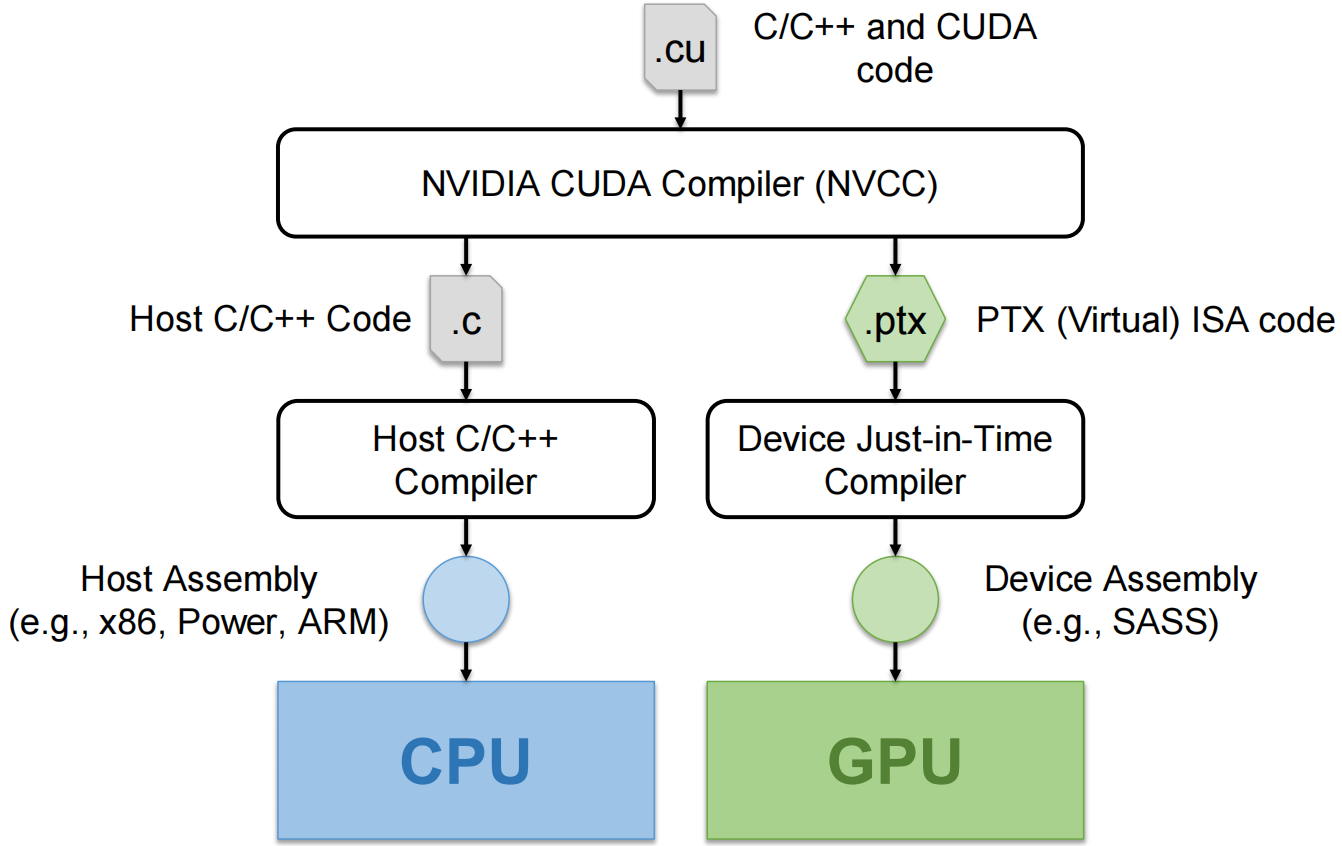
Function Declarations in CUDA

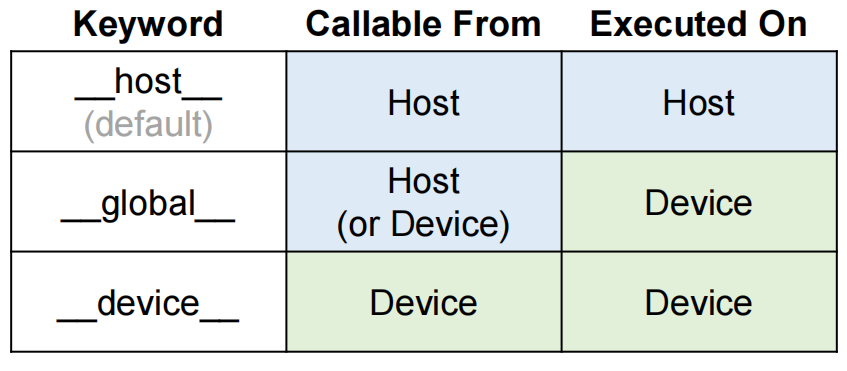
__global__ defines a kernel function

__device__ and __host__ can be used together

More on Function Declarations

The keyword __host__ is useful when needing to mark a function as executable on both the host and the device

__host__ __device__ float f(float a, float b) {
    return a + b;
}
void vecadd(float* x, float* y, float* z, int N) {
    for(unsigned int i = 0; i < N; ++i) {
        z[i] = f(x[i], y[i]);
    }
}
__global__ void vecadd_kernel(float* x, float* y, float* z, int N) {
    int i = blockDim.x*blockIdx.x + threadIdx.x;
    if (i < N) {
        z[i] = f(x[i], y[i]);
    }
}

Asynchronous Kernel Calls

By default, kernel calls are asynchronous 异步

• Useful for overlapping GPU computations with CPU computations

Use the following API function to wait for the kernel to finish

cudaError_t cudaDeviceSynchronize()

• Blocks until the device has completed all preceding requested tasks

Error Checking

All CUDA API calls return an error code cudaError_t that can be used to check if any errors occurred

cudaError_t err = ...;
if (err != cudaSuccess) {
    printf("Error: %s\n"
           , cudaGetErrorString(err));
    exit(0);
}

For kernel calls, one can check the error returned by cudaDeviceSynchronize() or call the following API function:cudaError_t cudaGetLastError()

Problems

CUDA Parallel Execution Model: Multidimensional Grids & Data

CUDA Thread Grids are Multi-Dimensional

CUDA supports multidimensional grids (up to 3D)

Each CUDA kernel is executed by a grid,

• a 3D array of thread blocks, which are 3D arrays of threads.
• Each thread executes the same program on distinct data inputs, a single-program, multiple-data (SPMD) model

Grid - block - thread

• gridDim - blockIdx - threadIdx

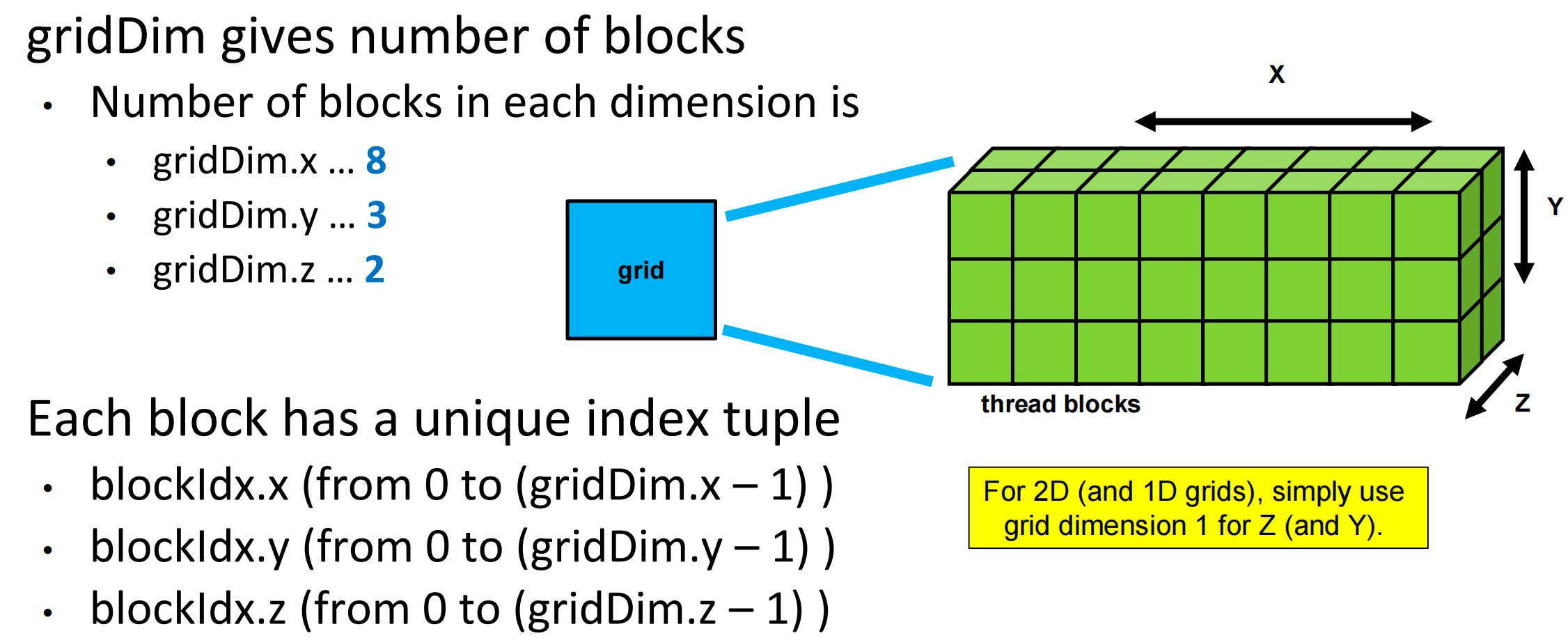
One Dimensional Indexing

Defining a working set for a thread

• i = blockIdx.x * blockDim.x + threadIdx.x;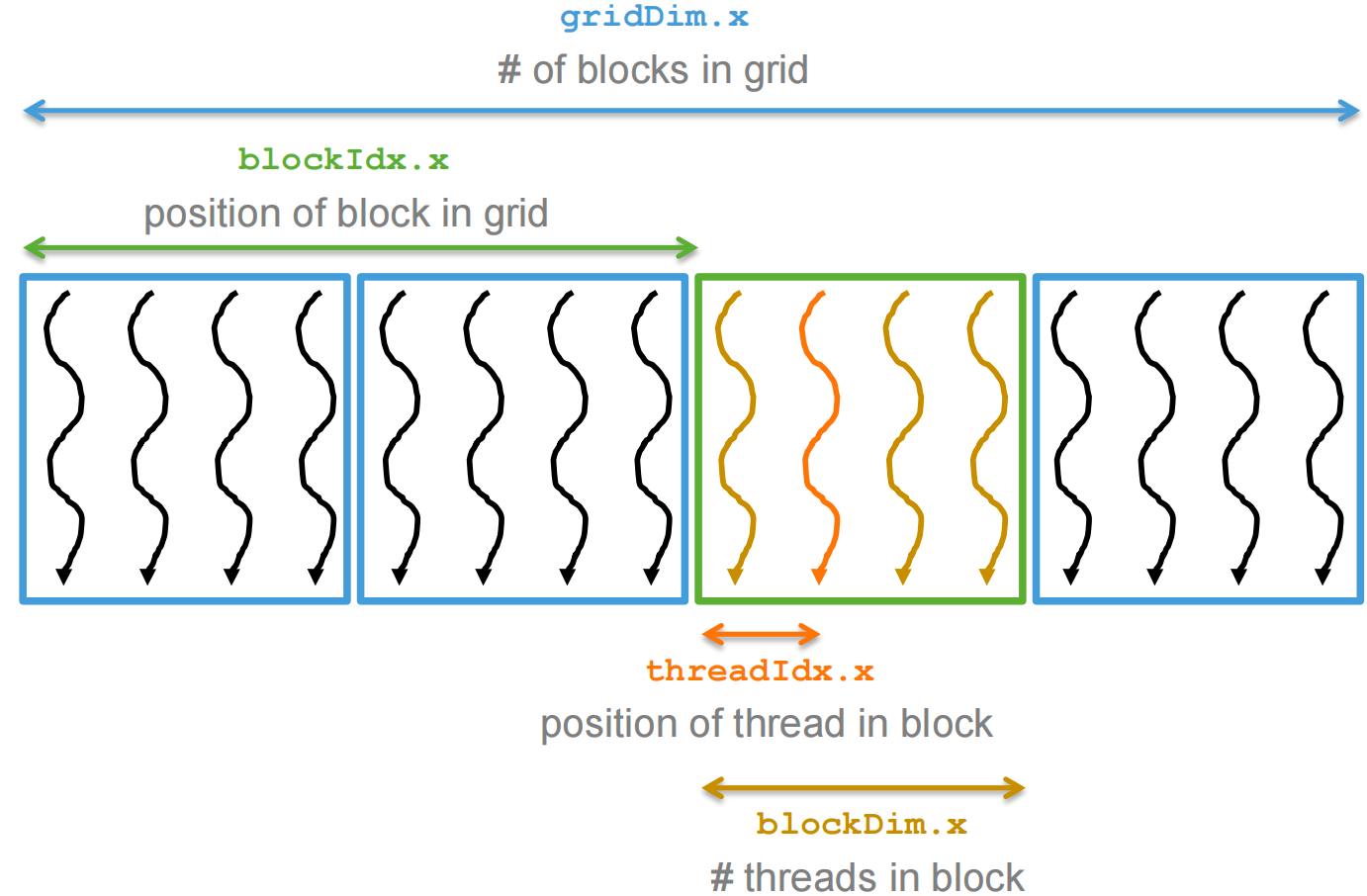
• 

Multidimensional Indexing

Defining a working set for a thread

• row = blockIdx.y * blockDim.y + threadIdx.y;
• col = blockIdx.x * blockDim.x + threadIdx.x;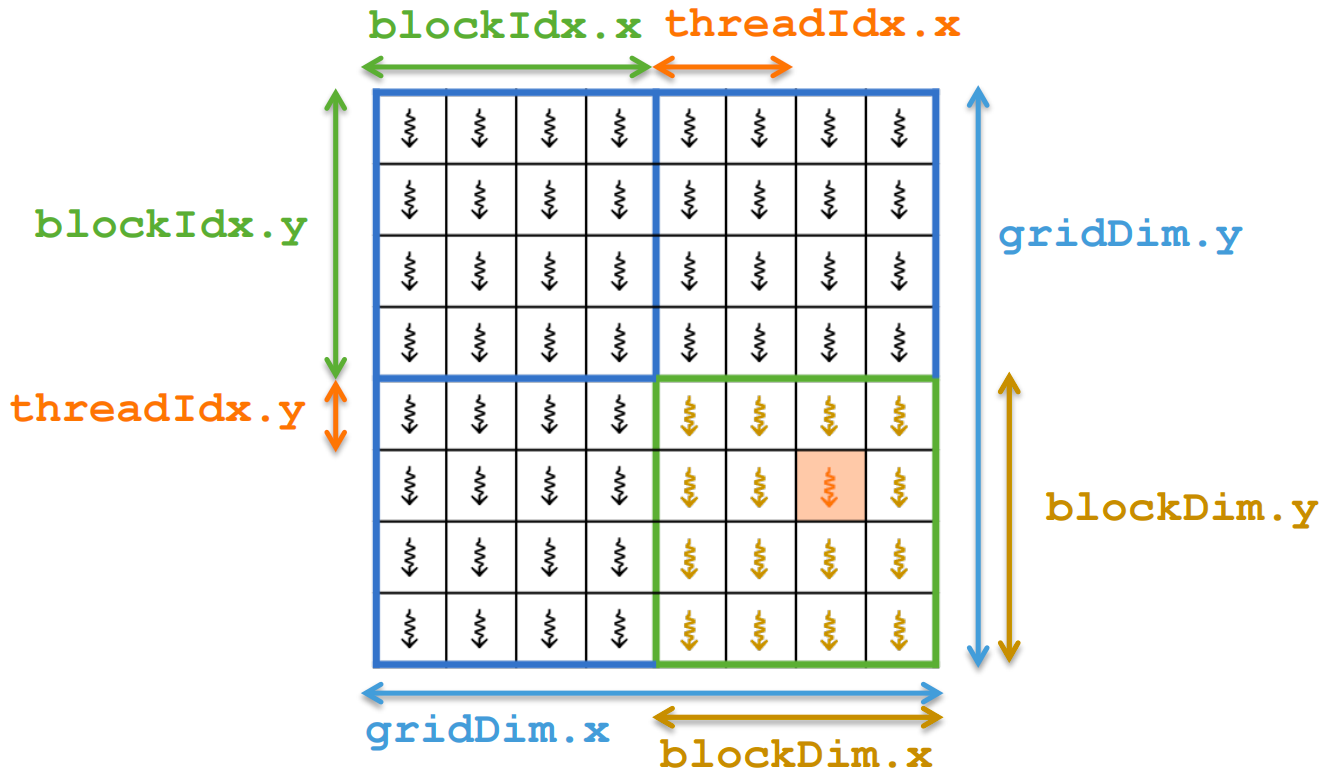
• 

Configuring Multidimensional Grids

Use built-in dim3 type

dim3 numThreadsPerBlock(32, 32); // 2D
dim3 numBlocks(
(width + numThreadsPerBlock.x - 1) / numThreadsPerBlock.x,
(height + numThreadsPerBlock.y - 1) / numThreadsPerBlock.y );
kernel <<< numBlocks, numThreadsPerBlock >>> (…kernel args…);

Layout of Multidimensional Data

• Convention is C is to store data in row major order
• Elements in the same row are contiguous in memory
• index = row * width + col

RGB to Gray-Scale Kernel Implementation

__global__
  void rgb2gray_kernel(unsigned char* red, unsigned char* green, unsigned char* blue, unsigned char* gray, unsigned int width, unsigned int height) 
{
  unsigned int row = blockIdx.y*blockDim.y + threadIdx.y;
  unsigned int col = blockIdx.x*blockDim.x + threadIdx.x;
  // Convert the pixel
  if (row < height && col < width) {
    gray[row*width + col] = red[row*width + col]*3/10
      + green[row*width + col]*6/10 + blue[row*width + col]*1/10;}
}

Blur Kernel Implementation

Parallelization approach: assign one thread to each output pixel, and have it read multiple input pixels

• Given two N × N matrices, A and B, we can multiply A by B to compute a third N × N matrix, P: P = AB

__global__ void blur_kernel(unsigned char* image, unsigned char* blurred, 
                            unsigned int width, unsigned int height) 
{
  int outRow = blockIdx.y*blockDim.y + threadIdx.y;
  int outCol = blockIdx.x*blockDim.x + threadIdx.x;
  if (outRow < height && outCol < width) 
  {
    unsigned int average = 0;
    for(int inRow = outRow - BLUR_SIZE; inRow < outRow + BLUR_SIZE + 1; ++inRow) {
      for(int inCol = outCol - BLUR_SIZE; inCol < outCol + BLUR_SIZE + 1; ++inCol) {
        if (inRow >= 0 && inRow < height && inCol >= 0 && inCol < width) {
average += image[inRow*width + inCol];
                }
      }
    }
    blurred[outRow*width + outCol] =
      (unsigned char)(average/((2*BLUR_SIZE + 1)*(2*BLUR_SIZE + 1)));
  }
}

[!NOTE]

Rule of thumb: every memory access must have a corresponding guard that compares its indexes to the array dimensions

Matrix-Matrix Multiplication

Given two N × N matrices, A and B, we can multiply A by B to compute a third N × N matrix, P: \(P = AB\)

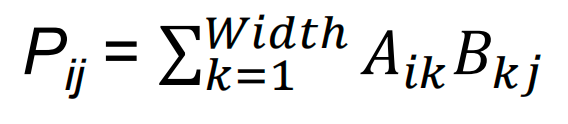• 矩阵相乘，一行✖️一列
• Parallelization approach: assign one threadto each element in the output matrix (C)

__global__ void mm_kernel(float* A, float* B, float* C, unsigned int N) 
{
  unsigned int row = blockIdx.y*blockDim.y + threadIdx.y;
  unsigned int col = blockIdx.x*blockDim.x + threadIdx.x;
  float sum = 0.0f;
  for(unsigned int i = 0; i < N; ++i) {
    sum += A[row*N + i]*B[i*N + col];
  }
  C[row*N + col] = sum;
}

评论区~

有用的话请给我个赞和 star =>